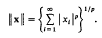Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Papini, Pier Luigi
1983.
Some parameters of Banach spaces.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 53,
Issue. 1,
p.
131.
Zhang, Yihan
and
Vatedka, Shashank
2023.
Multiple Packing:Lower Bounds via Infinite Constellations.
IEEE Transactions on Information Theory,
Vol. 69,
Issue. 7,
p.
4513.
Zhang, Yihan
and
Vatedka, Shashank
2024.
Multiple Packing: Lower Bounds via Error Exponents.
IEEE Transactions on Information Theory,
Vol. 70,
Issue. 2,
p.
1008.


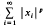 is convergent, with the norm defined by
is convergent, with the norm defined by