No CrossRef data available.
Article contents
The a-points of Faber polynomials for a special function†
Published online by Cambridge University Press: 18 May 2009
Extract
Let f(ζ) be a power series of the form

where lim sup |an|1/n < ∞. The Faber polynomials {fn(ζ)} (n = 0, 1, 2, …) are the polynomial parts of the formal expansion of (f(ζ))n about ζ = ∞. Series (1) defines an analytic element of an analytic function which we designate as w = f(ζ). Since 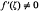 at ζ = ∞ the analytic element is univalent in some neighborhood of infinity; thus the inverse of this element is uniquely determined in some neighborhood of w= ∞, and has a Laurent expansion of the form
at ζ = ∞ the analytic element is univalent in some neighborhood of infinity; thus the inverse of this element is uniquely determined in some neighborhood of w= ∞, and has a Laurent expansion of the form

where lim sup |bn|1/n = p < ∞. Let ζ = g(w) be this single-valued function defined by (2) in |w| > p. No analytic continuation of g(w) will be considered.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1970


