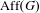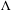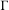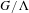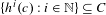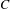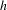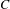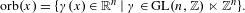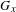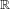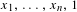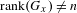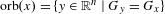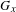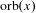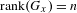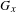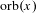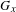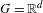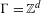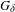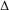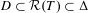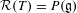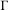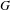Research Article
Rigidity for group actions on homogeneous spaces by affine transformations
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 2060-2076
-
- Article
- Export citation
Multifractal analysis for weak Gibbs measures: from large deviations to irregular sets
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 79-102
-
- Article
- Export citation
Subdiagrams and invariant measures on Bratteli diagrams
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 2417-2452
-
- Article
- Export citation
On a generalization of the Cartwright–Littlewood fixed point theorem for planar homeomorphisms
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1815-1824
-
- Article
-
- You have access
- Export citation
Non-divergence of unipotent flows on quotients of rank-one semisimple groups
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 103-128
-
- Article
- Export citation
A symbolic characterization of the horseshoe locus in the Hénon family
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1389-1412
-
- Article
- Export citation
Four-cycle free graphs, height functions, the pivot property and entropy minimality
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1102-1132
-
- Article
- Export citation
The parameter space of cubic laminations with a fixed critical leaf
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 2453-2486
-
- Article
- Export citation
Ziggurat fringes are self-similar
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 739-757
-
- Article
- Export citation
Transitive dendrite map with zero entropy
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 2077-2083
-
- Article
- Export citation
The local Hölder exponent for the dimension of invariant subsets of the circle
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1825-1840
-
- Article
-
- You have access
- Export citation
Plünnecke inequalities for measure graphs with applications
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 418-439
-
- Article
- Export citation
Measure evolution of cellular automata and of finitely anticipative transformations
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 129-145
-
- Article
- Export citation
Roots, Schottky semigroups, and a proof of Bandt’s conjecture
-
- Published online by Cambridge University Press:
- 13 July 2016, pp. 2487-2555
-
- Article
- Export citation
Stabilizers of actions of lattices in products of groups
-
- Published online by Cambridge University Press:
- 24 March 2016, pp. 1133-1186
-
- Article
- Export citation
Criteria for the density of the graph of the entropy map restricted to ergodic states
-
- Published online by Cambridge University Press:
- 29 January 2016, pp. 758-785
-
- Article
- Export citation
Incomparable actions of free groups
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 2084-2098
-
- Article
- Export citation
Classifying orbits of the affine group over the integers
-
- Published online by Cambridge University Press:
- 22 July 2015, pp. 440-453
-
- Article
- Export citation
Directional recurrence and directional rigidity for infinite measure preserving actions of nilpotent lattices
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1841-1861
-
- Article
-
- You have access
- Export citation
Continuity of Lyapunov exponents for random two-dimensional matrices
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1413-1442
-
- Article
- Export citation