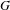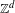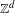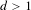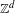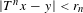Research Article
Weak Gibbs measures: speed of convergence to entropy, topological and geometrical aspects
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 2313-2336
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Closed orbits in quotient systems
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 2337-2352
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Whirly 3-interval exchange transformations
-
- Published online by Cambridge University Press:
- 20 October 2015, pp. 995-1008
-
- Article
- Export citation
On one-parameter Koopman groups
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 1635-1656
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 January 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
On intrinsic ergodicity of factors of
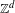 $\mathbb{Z}^{d}$ subshifts
$\mathbb{Z}^{d}$ subshifts
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 621-645
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 January 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 7 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 September 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
On shrinking targets for piecewise expanding interval maps
-
- Published online by Cambridge University Press:
- 25 August 2015, pp. 646-663
-
- Article
- Export citation
Weak mixing for locally compact quantum groups
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 1657-1680
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 7 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 September 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ETS volume 37 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Normality in Pisot numeration systems
-
- Published online by Cambridge University Press:
- 25 August 2015, pp. 664-672
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 July 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ETS volume 37 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 February 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 July 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ETS volume 37 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 February 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation