Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T02:11:44.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Roots, Schottky semigroups, and a proof of Bandt’s conjecture

Published online by Cambridge University Press:  13 July 2016

DANNY CALEGARI ,
SARAH KOCH  and
ALDEN WALKER
DANNY CALEGARI
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA email [email protected], [email protected]
SARAH KOCH
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA email [email protected]
ALDEN WALKER
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1985, Barnsley and Harrington defined a ‘Mandelbrot Set’ 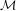${\mathcal{M}}$ for pairs of similarities: this is the set of complex numbers $z$ with 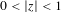$0<|z|<1$ for which the limit set of the semigroup generated by the similarities

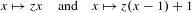$$\begin{eqnarray}x\mapsto zx\quad \text{and}\quad x\mapsto z(x-1)+1\end{eqnarray}$$
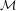is connected. Equivalently, ${\mathcal{M}}$ is the closure of the set of roots of polynomials with coefficients in 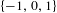$\{-1,0,1\}$. Barnsley and Harrington already noted the (numerically apparent) existence of infinitely many small ‘holes’ in 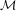${\mathcal{M}}$, and conjectured that these holes were genuine. These holes are very interesting, since they are ‘exotic’ components of the space of (2-generator) Schottky semigroups. The existence of at least one hole was rigorously confirmed by Bandt in 2002, and he conjectured that the interior points are dense away from the real axis. We introduce the technique of traps to construct and certify interior points of 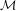${\mathcal{M}}$, and use them to prove Bandt’s conjecture. Furthermore, our techniques let us certify the existence of infinitely many holes in 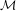${\mathcal{M}}$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 8 , December 2017 , pp. 2487 - 2555
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandt, C.. On the Mandelbrot set for pairs of linear maps. Nonlinearity 15 (2002), 1127–1147.Google Scholar
Barnsley, M. and Harrington, A.. A Mandelbrot set for pairs of linear maps. Phys. D. 15 (1985), 421–432.CrossRefGoogle Scholar
Bousch, T.. Paires de similitudes. Preprint, 1988; available from the author’s webpage http://topo.math.u-psud.fr/∼bousch/preprints/.Google Scholar
Bousch, T.. Connexité locale et par chemins hölderiens pour les systèmes itérés de fonctions. Preprint, 1992; available from the author’s webpage http://topo.math.u-psud.fr/∼bousch/preprints/.Google Scholar
Calegari, D. and Walker, A.. schottky, software available from https://github.com/dannycalegari/schottky.Google Scholar
Climenhaga, V. and Pesin, Y.. Lectures on Fractal Geometry and Dynamical Systems (Student Mathematical Library, 52) . American Mathematical Society, Providence, RI, 2009.Google Scholar
Epstein, D., Cannon, J., Holt, D., Levy, S., Paterson, M. and Thurston, W.. Word Processing in Groups. Jones and Bartlett, Burlington, MA, 1992.Google Scholar
Indlekofer, K., Járai, A. and Kátai, I.. On some properties of attractors generated by iterated function systems. Acta Sci. Math. (Szeged) 60 (1995), 411–427.Google Scholar
Mercat, P.. Semi-groupes fortement automatiques. Bull. Soc. Math. France 141 (2013), 423–479.Google Scholar
Odlyzko, A. and Poonen, B.. Zeros of polynomials with 0, 1 coefficients. Enseign. Math. 39 (1993), 317–348.Google Scholar
Shmerkin, P. and Solomyak, B.. Zeros of {-1, 0, 1} Power series and connectedness loci for self-affine sets. Exp. Math. 15 (2006), 499–511.Google Scholar
Solomyak, B.. Mandelbrot set for a pair of line maps: the local geometry. Anal. Theory Appl. 20 (2004), 149–157.Google Scholar
Solomyak, B.. On the ‘Mandelbrot set’ for pairs of linear maps: asymptotic self-similarity. Nonlinearity 18 (2005), 1927–1943.Google Scholar
Solomyak, B. and Xu, H.. On the ‘Mandelbrot set’ for a pair of linear maps and complex Bernoulli convolutions. Nonlinearity 16 (2003), 1733–1749.Google Scholar
Thurston, W.. Entropy in dimension one. Boundarys in Complex Dynamics: In Celebration of John Milnor’s 80th Birthday. Princeton University Press, Princeton, NJ, 2014, pp. 339–384.Google Scholar
Tiozzo, G.. Galois conjugates of entropies of real unimodal maps. Preprint, 2013, arXiv:1310.7647.Google Scholar