Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T01:53:30.257Z Has data issue: false hasContentIssue false
  • English
  • Français

Multifractal analysis for weak Gibbs measures: from large deviations to irregular sets

Published online by Cambridge University Press:  12 October 2015

THIAGO BOMFIM  and
PAULO VARANDAS
THIAGO BOMFIM
Affiliation:
Departamento de Matemática, Universidade Federal da Bahia, Av. Ademar de Barros s/n, 40170-110 Salvador, Brazil email [email protected], [email protected]
PAULO VARANDAS
Affiliation:
Departamento de Matemática, Universidade Federal da Bahia, Av. Ademar de Barros s/n, 40170-110 Salvador, Brazil email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

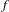In this article we prove estimates for the topological pressure of the set of points whose Birkhoff time averages are far from the space averages corresponding to the unique equilibrium state that has a weak Gibbs property. In particular, if $f$ has an expanding repeller and 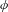$\unicode[STIX]{x1D719}$ is a Hölder continuous potential, we prove that the topological pressure of the set of points whose accumulation values of Birkhoff averages belong to some interval 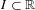$I\subset \mathbb{R}$ can be expressed in terms of the topological pressure of the whole system and the large deviations rate function. As a byproduct we deduce that most irregular sets for maps with the specification property have topological pressure strictly smaller than the whole system. Some extensions to a non-uniformly hyperbolic setting, level-2 irregular sets and hyperbolic flows are also given.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 1 , February 2017 , pp. 79 - 102
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J. F., Luzzatto, S., Freitas, J. and Vaienti, S.. From rates of mixing to recurrence times via large deviations. Adv. Math. 228 (2011), 1203–1236.Google Scholar
Barreira, L., Pesin, Y. and Schmeling, J.. Multifractal spectra and multifractal rigidity for horseshoes. J. Dyn. Control Syst. 3(1) (1997), 33–49.Google Scholar
Bomfim, T., Castro, A. and Varandas, P.. Differentiability of thermodynamical quantities in non-uniformly expanding dynamics. Preprint, 2012, arXiv:1205.5361.Google Scholar
Bomfim, T. and Varandas, P.. Multifractal analysis of the irregular set for almost-additive sequences via large deviations. Preprint, 2014, arXiv:1410.2220.Google Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Syst. Theory 8 (1974), 193–202.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, Berlin, 1975.Google Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29(3) (1975), 181–202.CrossRefGoogle Scholar
Bruin, H. and Todd, M.. Equilibrium states for interval maps: the potential - tlog|Df|. Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 559–600.Google Scholar
Castro, A. and Varandas, P.. Equilibrium states for non-uniformly expanding maps: decay of correlations and strong stability. Ann. Inst. H. Poincaré Anal. Non Linéaire 30(2) (2013), 225–249.Google Scholar
Castro, A. and Nascimento, T.. Statistical properties of equilibrium states for partially hyperbolic attractors. Preprint, UFBA, 2014.Google Scholar
Climenhaga, V.. Multifractal formalism derived from thermodynamics for general dynamical systems. Electron. Res. Announc. Math. Sci. 17 (2010), 1–11.Google Scholar
Climenhaga, V.. Topological pressure of simultaneous level sets. Nonlinearity 26 (2013), 241–268.CrossRefGoogle Scholar
Climenhaga, V., Thompson, D. and Yamamoto, K.. Large deviations for systems with non-uniform structure. Preprint, 2013, arXiv:1304.5497.Google Scholar
Comman, H. and Rivera-Letelier, J.. Large deviations principles for non-uniformly hyperbolic rational maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998), 539–579.Google Scholar
Denker, M. and Kesseböhmer, M.. Thermodynamical formalism, large deviation and multifractals. Stochastic Climate Models (Progress in Probability, 49) . Birkhäuser, Basel, 2001, pp. 159–169.Google Scholar
Díaz, L. and Gelfert, K.. Porcupine-like horseshoes: transitivity, Lyapunov spectrum, and phase transitions. Fund. Math. 216(1) (2012), 55–100.Google Scholar
Díaz, L., Gelfert, K. and Rams, M.. Rich phase transitions in step skew products. Nonlinearity 24(12) (2011), 3391–3412.Google Scholar
Eizenberg, A., Kifer, Y. and Weiss, B.. Large deviations for ℤ d actions. Comm. Math. Phys. 164 (1994), 433–454.CrossRefGoogle Scholar
Feng, D. and Huang, W.. Lyapunov spectrum of asymptotically sub-additive potentials. Comm. Math. Phys. 297 (2010), 1–43.Google Scholar
Gelfert, K. and Rams, M.. The Lyapunov spectrum of some parabolic systems. Ergod. Th. & Dynam. Sys. 29(3) (2009), 919–940.CrossRefGoogle Scholar
Hofbauer, F.. Examples for the nonuniqueness of the equilibrium state. Trans. Amer. Math. Soc. 228 (1977), 223–241.Google Scholar
Jordan, T. and Rams, M.. Multifractal analysis of weak Gibbs measures for non-uniformly expanding C 1 maps. Ergod. Th. & Dynam. Sys. 31(1) (2011), 143–164.Google Scholar
Kleptsyn, V., Ryzhov, D. and Minkov, S.. Special ergodic theorems and dynamical large deviations. Nonlinearity 25 (2012), 3189–3196.CrossRefGoogle Scholar
Melbourne, I.. Large and moderate deviations for slowly mixing dynamical systems. Proc. Amer. Math. Soc. 137 (2009), 1735–1741.Google Scholar
Melbourne, I. and Nicol, M.. Large deviations for nonuniformly hyperbolic systems. Trans. Amer. Math. Soc. 360 (2008), 6661–6676.Google Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems (Contemporary Views and Applications) . University of Chicago Press, Chicago, IL, 1997.Google Scholar
Pesin, Y. and Weiss, H.. The multifractal analysis of Gibbs measures: motivation, mathematical foundation, and examples. Chaos 7(1) (1997), 89–106.Google Scholar
Pfister, C. and Sullivan, W.. Large deviations estimates for dynamical systems without the specification property. Applications to the 𝛽-shifts. Nonlinearity 18 (2005), 237–261.Google Scholar
Pollicott, M. and Sharp, R.. Large deviations for intermittent maps. Nonlinearity 22 (2009), 2079–2092.Google Scholar
Pollicott, M. and Weiss, H.. Multifractal analysis of Lyapunov exponent for continued fraction and Manneville–Pomeau transformations and applications to Diophantine approximation. Comm. Math. Phys. 207 (1999), 145–171.CrossRefGoogle Scholar
Rey-Bellet, L. and Young, L.-S.. Large deviations in non-uniformly hyperbolic dynamical systems. Ergod. Th. & Dynam. Sys. 28 (2008), 587–612.Google Scholar
Takens, F. and Verbitski, E.. Multifractal analysis of local entropies for expansive homeomorphisms with specification. Comm. Math. Phys. 203 (1999), 593–612.Google Scholar
Thompson, D.. A variational principle for topological pressure for certain non-compact sets. J. Lond. Math. Soc. 80(3) (2009), 585–602.Google Scholar
Todd, M.. Multifractal analysis for multimodal maps. Preprint, 2008.Google Scholar
Thompson, D.. The irregular set for maps with the specification property has full topological pressure. Dyn. Syst. 25(1) (2010), 25–51.Google Scholar
Varandas, P.. Non-uniform specification and large deviations for weak Gibbs measures. J. Stat. Phys. 146 (2012), 330–358.Google Scholar
Varandas, P. and Viana, M.. Existence, uniqueness and stability of equilibrium states for non-uniformly expanding maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 27 (2010), 555–593.Google Scholar
Young, L.-S.. Some large deviations for dynamical systems. Trans. Amer. Math. Soc. 318 (1990), 525–543.Google Scholar
Zhou, X. and Chen, E.. Multifractal analysis for the historic set in topological dynamical systems. Nonlinearity 26(7) (2013), 1975–1997.Google Scholar