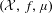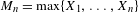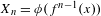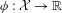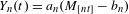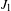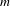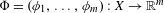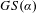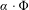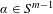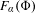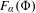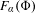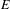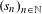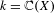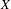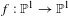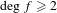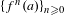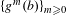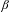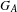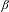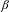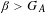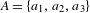Original Article
Normal amenable subgroups of the automorphism group of the full shift
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 1290-1298
-
- Article
- Export citation
A necessary and sufficient condition for a matrix equilibrium state to be mixing
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 2223-2234
-
- Article
- Export citation
Local rigidity of higher rank non-abelian action on torus
-
- Published online by Cambridge University Press:
- 25 September 2017, pp. 1668-1709
-
- Article
- Export citation
Weak convergence to extremal processes and record events for non-uniformly hyperbolic dynamical systems
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 980-1001
-
- Article
- Export citation
Dimensions of an overlapping generalization of Barański carpets
-
- Published online by Cambridge University Press:
- 25 September 2017, pp. 733-763
-
- Article
- Export citation
Incompleteness of the pressure metric on the Teichmüller space of a bordered surface
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 1710-1728
-
- Article
- Export citation
Optimal state amalgamation is NP-hard
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 1857-1869
-
- Article
- Export citation
Ground states and zero-temperature measures at the boundary of rotation sets
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 201-224
-
- Article
- Export citation
Dimension of harmonic measures in hyperbolic spaces
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 474-499
-
- Article
- Export citation
Weak colored local rules for planar tilings
-
- Published online by Cambridge University Press:
- 05 April 2018, pp. 3322-3346
-
- Article
- Export citation
Recurrence, rigidity, and popular differences
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 1299-1316
-
- Article
- Export citation
 $J$-stability of expanding maps in non-Archimedean dynamics
$J$-stability of expanding maps in non-Archimedean dynamics
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1002-1019
-
- Article
- Export citation
Rationality of dynamical canonical height
-
- Published online by Cambridge University Press:
- 18 January 2018, pp. 2507-2540
-
- Article
- Export citation
Sturmian words and Cantor sets arising from unique expansions over ternary alphabets
-
- Published online by Cambridge University Press:
- 25 January 2018, pp. 2827-2854
-
- Article
- Export citation
Li–Yorke sensitivity does not imply Li–Yorke chaos
-
- Published online by Cambridge University Press:
- 06 March 2018, pp. 3066-3074
-
- Article
- Export citation
Fatou components of elliptic polynomial skew products
-
- Published online by Cambridge University Press:
- 28 November 2017, pp. 2235-2247
-
- Article
- Export citation
Mean topological dimension for random bundle transformations
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1020-1041
-
- Article
- Export citation
A counterexample to the composition condition conjecture for polynomial Abel differential equations
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3347-3352
-
- Article
- Export citation
Continued fraction algorithm for Sturmian colorings of trees
-
- Published online by Cambridge University Press:
- 12 December 2017, pp. 2541-2569
-
- Article
- Export citation
Lyapunov-maximizing measures for pairs of weighted shift operators
-
- Published online by Cambridge University Press:
- 04 May 2017, pp. 225-247
-
- Article
- Export citation