Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T04:28:37.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Sturmian words and Cantor sets arising from unique expansions over ternary alphabets

Published online by Cambridge University Press:  25 January 2018

DOYONG KWON
DOYONG KWON*
Affiliation:
Department of Mathematics, Chonnam National University, Gwangju 61186, Republic of Korea email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Over a finite alphabet $A$ of real numbers, unique expansions in base 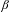$\unicode[STIX]{x1D6FD}$ are considered. A real number 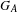$G_{A}$ called the generalized golden ratio is a critical point of a situation of unique expansions. If 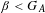$\unicode[STIX]{x1D6FD}<G_{A}$, then there are only trivial unique expansions in base 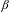$\unicode[STIX]{x1D6FD}$, while there are non-trivial unique expansions in base 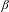$\unicode[STIX]{x1D6FD}$ whenever $\unicode[STIX]{x1D6FD}>G_{A}$. Komornik, Lai and Pedicini [Generalized golden ratios of ternary alphabets. J. Eur. Math. Soc.13(4) (2011), 1113–1146] investigated the case where $A$ consists of three real numbers, and demonstrated that Sturmian words curiously emerge out of the generalized golden ratio. The present paper focuses on Sturmian words under this context. For a given alphabet 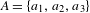$A=\{a_{1},a_{2},a_{3}\}$ with $a_{1}<a_{2}<a_{3}$, we give a complete characterization of the corresponding Sturmian words effectively and algorithmically, which reveals interesting structures behind the generalized golden ratios.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 10 , October 2019 , pp. 2827 - 2854
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P. and Glen, A.. Distribution modulo 1 and the lexicographic world. Ann. Sci. Math. Québec 33(2) (2009), 125–143.Google Scholar
Baker, S. and Steiner, W.. On the regularity of the generalised golden ratio function. Bull. Lond. Math. Soc. 49(1) (2017), 58–70.Google Scholar
Berstel, J., Lauve, A., Reutenauer, C. and Saliola, F. V.. Combinatorics on Words. Christoffel Words and Repetitions in Words. American Mathematical Society, Providence, RI, 2009.Google Scholar
Blanchard, F.. 𝛽-expansions and symbolic dynamics. Theoret. Comput. Sci. 65(2) (1989), 131–141.Google Scholar
Borel, J.-P. and Laubie, F.. Quelques mots sur la droite projective réelle. J. Théor. Nombres Bordeaux 5(1) (1993), 23–51.Google Scholar
Brown, G. and Yin, Q.. 𝛽-transformation, natural extension and invariant measure. Ergod. Th. & Dynam. Sys. 20(5) (2000), 1271–1285.Google Scholar
Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots, and the devil’s staircase. Math. Proc. Cambridge Philos. Soc. 115(3) (1994), 451–481.Google Scholar
Daróczy, Z. and Kátai, I.. Univoque sequences. Publ. Math. Debrecen 42(3–4) (1993), 397–407.Google Scholar
Erdös, P., Joó, I. and Komornik, V.. Characterization of the unique expansions 1 =∑ i=1 ∞ q -n i and related problems. Bull. Soc. Math. France 118(3) (1990), 377–390.Google Scholar
Falconer, K.. Fractal Geometry. Mathematical Foundations and Applications, 2nd edn. John Wiley & Sons, Hoboken, NJ, 2003.Google Scholar
Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, 6th edn. Oxford University Press, Oxford, 2008.Google Scholar
Komornik, V., Lai, A. C. and Pedicini, M.. Generalized golden ratios of ternary alphabets. J. Eur. Math. Soc. 13(4) (2011), 1113–1146.Google Scholar
Kwon, D. Y.. The natural extensions of 𝛽-transformations which generalize baker’s transformations. Nonlinearity 22(2) (2009), 301–310.Google Scholar
Kwon, D. Y.. The orbit of a 𝛽-transformation cannot lie in a small interval. J. Korean Math. Soc. 49(4) (2012), 867–879. Addendum is available at www.math.jnu.ac.kr/doyong/paper/AddOrdered-June2016.pdf.Google Scholar
Kwon, D. Y.. Moments of discrete measures with dense jumps induced by 𝛽-expansions. J. Math. Anal. Appl. 399(1) (2013), 1–11.Google Scholar
Lai, A. C.. Minimal unique expansions with digits in ternary alphabets. Indag. Math. (N.S.) 21(1–2) (2011), 1–15.Google Scholar
Lind, D. A.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod. Th. & Dynam. Sys. 4(2) (1984), 283–300.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words. Cambridge University Press, Cambridge, 2002.Google Scholar
Loxton, J. H. and van der Poorten, A. J.. Arithmetic properties of certain functions in several variables. III. Bull. Aust. Math. Soc. 16(1) (1977), 15–47.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Parry, W.. On the 𝛽-expansion of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.Google Scholar