Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T04:42:56.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Li–Yorke sensitivity does not imply Li–Yorke chaos

Published online by Cambridge University Press:  06 March 2018

JANA HANTÁKOVÁ
JANA HANTÁKOVÁ*
Affiliation:
Mathematical Institute, Silesian University, 746 01 Opava, Czech Republic email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct an infinite-dimensional compact metric space 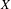$X$, which is a closed subset of 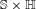$\mathbb{S}\times \mathbb{H}$, where $\mathbb{S}$ is the unit circle and 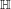$\mathbb{H}$ is the Hilbert cube, and a skew-product map $F$ acting on 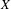$X$ such that 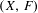$(X,F)$ is Li–Yorke sensitive but possesses at most countable scrambled sets. This disproves the conjecture of Akin and Kolyada that Li–Yorke sensitivity implies Li–Yorke chaos [Akin and Kolyada. Li–Yorke sensitivity. Nonlinearity16, (2003), 1421–1433].

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 3066 - 3074
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E. and Kolyada, S.. Li–Yorke sensitivity. Nonlinearity 16 (2003), 1421–1433.Google Scholar
Auslander, J. and Yorke, J.. Interval maps, factors of maps, and chaos. Tôhoku Math. J. 32 (1980), 177–188.Google Scholar
Čiklová, M.. Li–Yorke sensitive minimal maps. Nonlinearity 19 (2006), 517–529.Google Scholar
Čiklová-Mlíchová, M.. Li–Yorke sensitive minimal maps II. Nonlinearity 22 (2009), 1569–1573.Google Scholar
Devaney, R. L.. An Introduction to Chaotic Dynamical Systems (Addison-Wesley Studies in Nonlinearity) . Addison-Wesley, Redwood City, CA, 1989.Google Scholar
Huang, W. and Ye, X.. Devaney’s chaos or 2-scattering implies Li–Yorke’s chaos. Topology Appl. 117 (2002), 259–272.Google Scholar
Li, J. and Ye, X.. Recent development of chaos theory in topological dynamics. Acta Math. Sin. (Engl. Ser.) 32 (2016), 83–114.Google Scholar
Li, T. and Yorke, J.. Period three implies chaos. Amer. Math. Monthly 82 (1975), 985–992.Google Scholar
Lorenz, E. N.. Deterministic nonperiodic flow. J. Atmos. Sci. 20 (1963), 130–148.Google Scholar
Shao, S. and Ye, X.. A non-PI minimal system is Li–Yorke sensitive. Proc. Amer. Math. Soc. doi:10.1090/proc/13779, Published online September 2017.Google Scholar