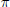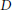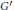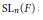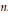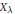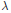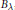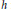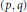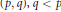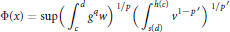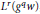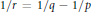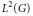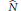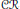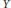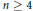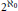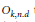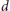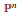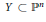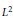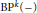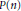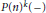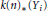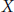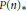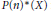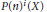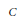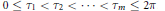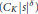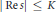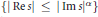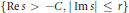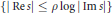Research Article
Harmonic Analysis on Metrized Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-275
-
- Article
-
- You have access
- Export citation
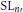 $S{{L}_{n\prime }}$ Orthogonality Relations and Transfer
$S{{L}_{n\prime }}$ Orthogonality Relations and Transfer
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-464
-
- Article
-
- You have access
- Export citation
Hecke
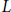 $L$-Functions and the Distribution of Totally Positive Integers
$L$-Functions and the Distribution of Totally Positive Integers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-695
-
- Article
-
- You have access
- Export citation
The Ground State Problem for a Quantum Hamiltonian Model Describing Friction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-916
-
- Article
-
- You have access
- Export citation
Meromorphic Continuation of Spherical Cuspidal Data Eisenstein Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1121-1134
-
- Article
-
- You have access
- Export citation
Holomorphic Generation of Continuous Inverse Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-35
-
- Article
-
- You have access
- Export citation
Sobolev Extensions of Hölder Continuous and Characteristic Functions on Metric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1135-1153
-
- Article
-
- You have access
- Export citation
Classification of Ding's Schubert Varieties: Finer Rook Equivalence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 36-62
-
- Article
-
- You have access
- Export citation
Weighted Inequalities for Hardy–Steklov Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 276-295
-
- Article
-
- You have access
- Export citation
Admissibility for a Class of Quasiregular Representations
-
- Published online by Cambridge University Press:
- 18 June 2019, pp. 917-942
-
- Article
-
- You have access
- Export citation
Searching for Absolute
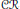 $\mathcal{C}\mathcal{R}$-Epic Spaces
$\mathcal{C}\mathcal{R}$-Epic Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-487
-
- Article
-
- You have access
- Export citation
Algèbres de Lie d'homotopie associées à une proto-bigèbre de Lie
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 696-711
-
- Article
-
- You have access
- Export citation
Some Results on the Schroeder–Bernstein Property for Separable Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-84
-
- Article
-
- You have access
- Export citation
Osculating Varieties of Veronese Varieties and Their Higher Secant Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 488-502
-
- Article
-
- You have access
- Export citation
A Weighted
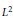 ${{L}^{2}}$-Estimate of the Witten Spinor in Asymptotically Schwarzschild Manifolds
${{L}^{2}}$-Estimate of the Witten Spinor in Asymptotically Schwarzschild Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 943-965
-
- Article
-
- You have access
- Export citation
k(n)-Torsion-Free H-Spaces and P(n)-Cohomology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1154-1206
-
- Article
-
- You have access
- Export citation
Bol Loops of Nilpotence Class Two
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 296-310
-
- Article
-
- You have access
- Export citation
Jet Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 712-729
-
- Article
-
- You have access
- Export citation
Large Sieve Inequalities via Subharmonic Methods and the Mahler Measure of the Fekete Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 730-741
-
- Article
-
- You have access
- Export citation
Growth and Zeros of the Zeta Function for Hyperbolic Rational Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 311-331
-
- Article
-
- You have access
- Export citation