Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T19:34:52.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Osculating Varieties of Veronese Varieties and Their Higher Secant Varieties

Published online by Cambridge University Press:  20 November 2018

A. Bernardi ,
M. V. Catalisano ,
A. Gimigliano  and
M. Idà
A. Bernardi
Affiliation:
Dipartimento di Matematica di Bologna, Porta San Donato 5, 40126, Bologna, Italia email: [email protected]
M. V. Catalisano
Affiliation:
DIPTEM, Università di Genova, Genova, Italia email: [email protected]
A. Gimigliano
Affiliation:
Dipartimento di Matematica and C.I.R.A.M., Università di Bologna, Bologna, Italia email: [email protected]
M. Idà
Affiliation:
Dipartimento di Matematica, Università di Bologna, Bologna, Italia email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

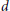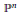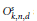We consider the $k$-osculating varieties ${{O}_{k,\,n.d}}$ to the (Veronese) $d$-uple embeddings of ${{\mathbb{P}}^{n}}$. We study the dimension of their higher secant varieties via inverse systems (apolarity). By associating certain 0-dimensional schemes $Y\,\subset \,{{\mathbb{P}}^{n}}$ to $O_{k,n,d}^{s}$ and by studying their Hilbert functions, we are able, in several cases, to determine whether those secant varieties are defective or not.

Keywords

14N1515A69
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 3 , 01 June 2007 , pp. 488 - 502
Copyright
Copyright © Canadian Mathematical Society 2007

References

[A] Ådlandsvik, B., Varieties with an extremal number of degenerate higher secant varieties. J. Reine Angew. Math. 392(1988), 16–26.Google Scholar
[AH] Alexander, J. and Hirschowitz, A., Polynomial interpolation in several variables. J. Algebraic Geom. 4(1995), no. 2, 201–222.Google Scholar
[B] Ballico, E., On the secant varieties to the tangent developable of a Veronese variety. J. Algebra 288(2005), no. 2, 279–286.Google Scholar
[BF] Ballico, E. and Fontanari, C., On the secant varieties to the osculating variety of a Veronese surface. Cent. Eur. J. Math. 1(2003), no. 3, 315–326.Google Scholar
[BF2] Ballico, E. and Fontanari, C., A Terracini lemma for osculating spaces with applications to Veronese surfaces. J. Pure Appl. Algebra 195(2005), no. 1, 1–6.Google Scholar
[Be] Bernardi, A., Varieties Parameterizing Forms and Their Secant Varieties. Tesi di Dottorato, Universit á di Milano.Google Scholar
[BC] Bernardi, A. and Catalisano, M. V., Some defective secant varieties to osculating varieties of Veronese surfaces. Collect. Math. 57(2006), no. 1, 43–68.Google Scholar
[CGG] Catalisano, M. V., Geramita, A. V., and Gimigliano, A.. On the secant varieties to the tangential varieties of a Veronesean. Proc. Amer. Math. Soc. 130(2002), 975–985.Google Scholar
[CCMO] Ciliberto, C., Cioffi, F., Miranda, R., and Orecchia, F., Bivariate Hermite interpolation and linear systems of plane curves with base fat points. In: Computer Mathematics, Lecture Notes Series on Computing 10, World Scientific Publ., River Edge, NJ, 2003, pp. 87–102.Google Scholar
[Ge] Geramita, A. V., Inverse Systems of Fat Points. Queen's Papers in Pure Appl. Math. 102(1998), 3–104.Google Scholar
[Ha] Harbourne, B., Problems and progress: A survey on fat points i. ℙ2. Queen's Papers in Pure Appl. Math. 123(2002), 87–132.Google Scholar
[Hi] Hirschowitz, A., La méthode de Horace pour l’interpolation à plusieurs variables. Manuscripta Math. 50(1985), 337–388.Google Scholar
[I] Iarrobino, A., Inverse systems of a symbolic power. III. Thin algebras and fat points. Compositio Math. 108(1997), no. 3, 319–356.Google Scholar
[IK] Iarrobino, A. and Kanev, V., Power Sums, Gorenstein Algebras, and Determinantal Loci. Lecture Notes in Mathematics 1721, Springer-Verlag, Berlin, 1999.Google Scholar
[Se] Segre, B., Un’estensione delle varietà di Veronese ed un principio di dualità per le forme algebriche. I and II. ti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat.(8) 1(1946), 313–318; 559–563.Google Scholar
[Te] Terracini, A., Sulle Vk per cui la varietà degli Sh (h + 1)-seganti ha dimensione minore dell’ordinario. Rend. Circ. Mat. Palermo 31(1911), 392–396.Google Scholar
[W] Wakeford, K., On canonical forms. Proc. London Math. Soc. (2) 18(1919/20), 403–410.Google Scholar