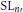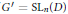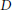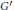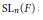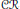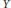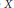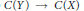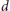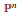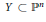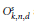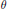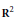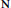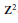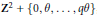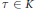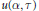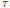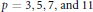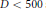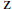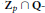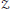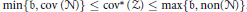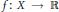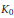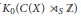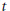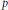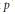Research Article
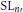 $S{{L}_{n\prime }}$ Orthogonality Relations and Transfer
$S{{L}_{n\prime }}$ Orthogonality Relations and Transfer
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-464
-
- Article
-
- You have access
- Export citation
Searching for Absolute
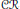 $\mathcal{C}\mathcal{R}$-Epic Spaces
$\mathcal{C}\mathcal{R}$-Epic Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-487
-
- Article
-
- You have access
- Export citation
Osculating Varieties of Veronese Varieties and Their Higher Secant Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 488-502
-
- Article
-
- You have access
- Export citation
Cyclic Groups and the Three Distance Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-552
-
- Article
-
- You have access
- Export citation
Computations of Elliptic Units for Real Quadratic Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 553-574
-
- Article
-
- You have access
- Export citation
Cardinal Invariants of Analytic
 $P$-Ideals
$P$-Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 575-595
-
- Article
-
- You have access
- Export citation
Eigenvalues,
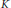 $K$-theory and Minimal Flows
$K$-theory and Minimal Flows
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-613
-
- Article
-
- You have access
- Export citation
Preduals and Nuclear Operators Associated with Bounded,
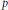 $p$-Convex,
$p$-Convex, 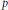 $p$-Concave and Positive
$p$-Concave and Positive 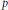 $p$-Summing Operators
$p$-Summing Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 614-637
-
- Article
-
- You have access
- Export citation
Distance from Idempotents to Nilpotents
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 638-657
-
- Article
-
- You have access
- Export citation
Division Algebras of Prime Degree and Maximal Galois
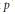 $p$-Extensions
$p$-Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-672
-
- Article
-
- You have access
- Export citation