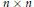Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Skoufranis, Paul
2013.
Normal Limits of Nilpotent Operators in von Neumann Algebras.
Integral Equations and Operator Theory,
Vol. 77,
Issue. 3,
p.
407.
Cramer, Zachary
2021.
The Distance from a Rank Projection to the Nilpotent Operators on .
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 1,
p.
54.
Mori, Michiya
2023.
On the distance from a matrix to nilpotents.
Linear Algebra and its Applications,
Vol. 679,
Issue. ,
p.
99.