Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T19:06:13.903Z Has data issue: false hasContentIssue false
  • English
  • Français

Preduals and Nuclear Operators Associated with Bounded, 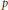$p$-Convex, 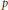$p$-Concave and Positive 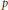$p$-Summing Operators

Published online by Cambridge University Press:  20 November 2018

C. C. A. Labuschagne
C. C. A. Labuschagne*
Affiliation:
School of Mathematics, University of the Witwatersrand, South Africa email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use Krivine's form of the Grothendieck inequality to renorm the space of bounded linear maps acting between Banach lattices. We construct preduals and describe the nuclear operators associated with these preduals for this renormed space of bounded operators as well as for the spaces of 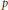$p$-convex, 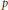$p$-concave and positive 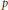$p$-summing operators acting between Banach lattices and Banach spaces. The nuclear operators obtained are described in terms of factorizations through classical Banach spaces via positive operators.

Keywords

46B2847B1046B4246B45p-convex operatorp-concave operatorp-summing operatorBanach spaceBanach latticenuclear operatorsequence space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 3 , 01 June 2007 , pp. 614 - 637
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Blasco, O., Positive p-summing operators on Lp-spaces. Proc. Amer. Math. Soc. 100(1987), 275–280.Google Scholar
[2] Bu, Q. and Buskes, G., The Radon-Nikodým property for tensor products of Banach lattices. Positivity 10(2006), no. 2, 365–390.Google Scholar
[3] Chaney, J., Banach lattices of compact maps. Math. Z. 129(1972), 1–19.Google Scholar
[4] Chevet, S., Sur certains produits tensoriels topologiques d’espaces de Banach. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 11(1969), 120–138.Google Scholar
[5] Cohen, J. S., Absolutely p-summing, p-nuclear operators and their conjugates. Math. Ann. 201(1973), 177–200.Google Scholar
[6] Defant, A. and Floret, K., Tensor Norms and Operator Ideals. North-Holland Mathematics Studies 176, North-Holland Publishing, Amsterdam, 1993.Google Scholar
[7] Diestel, J., Sequence Spaces and Series in Banach spaces. Graduate Texts in Mathematics 92, Springer-Verlag, New York, 1984.Google Scholar
[8] Diestel, J., Fourie, J. H. and Swart, J., The metric theory of tensor products. I and II. Quaest. Math. 25(2002), no. 1, 37–94.Google Scholar
[9] Diestel, J., Jarchow, H. and Tonge, A., Absolutely Summing Operators. Cambridge Studies in Advanced Mathematics 43, Cambridge University Press, Cambridge, 1995.Google Scholar
[10] Diestel, J. and Uhl, J. J., Vector Measures. Mathematical Surveys 15, American Mathematical Society, Providence, RI, 1977.Google Scholar
[11] Fourie, J. H. and Swart, J., Banach ideals of p-compact operators. Manuscripta Math. 26(1978/79), no. 4, 349–362.Google Scholar
[12] Fourie, J. H. and Swart, J., Tensor Products and Banach Ideals of p-compact operators. Manuscripta Math. 35(1981), no. 3, 343–351.Google Scholar
[13] Fremlin, D. H., Tensor products of Archimedean vector lattices. Amer. J. Math. 94(1972), 778–798.Google Scholar
[14] Grothendieck, A., Résumé de la théorie métrique des produits tensoriels topologiques. Bol. Soc. Mat. São Paulo 8(1953), 1–79.Google Scholar
[15] Jacobs, H., Ordered Topological Tensor Products. Ph.D. Thesis, University of Illinois, 1969.Google Scholar
[16] Jarchow, H., Locally convex spaces. B. G. Teubner, Stuttgart, 1981.Google Scholar
[17] Jeurnink, G. A. M., Integration of Functions with Values in a Banach Lattice. Thesis, University of Nijmegen, The Netherlands, 1982.Google Scholar
[18] Krivine, J. L., Thèorèmes de factorisation dans les espaces réticulés. Séminaire Maurey-Schwartz (1973-74), Exposes 22-23, école Polytechnique, Paris, 1974.Google Scholar
[19] Kwapien, S., On operators factoring through Lp spaces. In: Actes du Colloque d’Analyse Fonctionnelle de Bordeaux, Bull. Soc. Math. France, Mém. no. 31–32. Soc. Math. France, Paris, 1972, pp. 215–225.Google Scholar
[20] Labuschagne, C. C. A., Riesz reasonable cross norms on tensor products of Banach lattices. Quaest. Math. 27(2004), 243–266.Google Scholar
[21] Labuschagne, C. C. A., Characterizing the one-sided tensor norms Δp and tΔp . Quaest. Math. 27(2004), no. 4, 339–363.Google Scholar
[22] Lindenstrauss, Y. and Tzafriri, L., Classical Banach Spaces. II.Function spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 97, Springer-Verlag, Berlin, 1979.Google Scholar
[23] Meyer-Nieberg, P., Banach Lattices. Springer-Verlag, Berlin, 1991.Google Scholar
[24] Pietsch, A., Operator Ideals. North-Holland, Amsterdam, 1980.Google Scholar
[25] Pisier, G., Factorization of Linear Operators and Geometry of Banach Spaces. CBMS Regional Conference Series in Mathematics 60. American Mathematical Society, Providence, RI, 1986.Google Scholar
[26] Ryan, R. A., Introduction to tensor products of Banach spaces. Springer-Verlag, London, 2002.Google Scholar
[27] Saphar, P., Applications à puissance nucléaire et applications de Hilbert-Schmidt dans les espaces de Banach. Ann. Sci. école Norm. Sup. 83(1966) 113–151.Google Scholar
[28] Saphar, P., Produits tensoriels d’espaces de Banach et classes d’applications linéaires. Studia Math. 38(1970), 71–100.Google Scholar
[29] Schaefer, H. H., Banach Lattices and Positive Operators. Grundlehren der Mathematischen Wissenschaften 215, Springer-Verlag, New York, 1974.Google Scholar
[30] Zaanen, A. C., Introduction to Operator Theory in Riesz Spaces. Springer-Verlag, New York, 1997.Google Scholar