Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T23:04:19.139Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Ding's Schubert Varieties: Finer Rook Equivalence

Published online by Cambridge University Press:  20 November 2018

Mike Develin ,
Jeremy L. Martin  and
Victor Reiner
Mike Develin
Affiliation:
American Institute of Mathematics 360 Portage Ave. Palo Alto, CA 94306-2244 U.S.A. e-mail: [email protected]
Jeremy L. Martin
Affiliation:
Department of Mathematics University of Kansas Lawrence, KS 66045 U.S.A. e-mail: [email protected]
Victor Reiner
Affiliation:
School of Mathematics University of Minnesota Minneapolis, MN 55455 U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

K. Ding studied a class of Schubert varieties 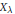${{X}_{\lambda }}$ in type A partial flag manifolds, indexed by integer partitions $\text{ }\!\!\lambda\!\!\text{ }$ and in bijection with dominant permutations. He observed that the Schubert cell structure of 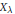${{X}_{\lambda }}$ is indexed by maximal rook placements on the Ferrers board 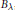${{B}_{\lambda \text{ }}}$, and that the integral cohomology groups 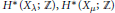${{H}^{*}}\left( {{X}_{\lambda }};\,\mathbb{Z} \right),\,{{H}^{*}}\left( {{X}_{\mu }};\,\mathbb{Z} \right)$ are additively isomorphic exactly when the Ferrers boards 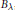${{B}_{\lambda \text{ }}}$, 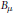${{B}_{\mu }}$ satisfy the combinatorial condition of rook-equivalence.

We classify the varieties 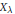${{X}_{\lambda }}$ up to isomorphism, distinguishing them by their graded cohomology rings with integer coefficients. The crux of our approach is studying the nilpotence orders of linear forms in the cohomology ring.

Keywords

14M1505E05Schubert varietyrook placementFerrers boardflag manifoldcohomology ringnilpotence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 1 , 01 February 2007 , pp. 36 - 62
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Cox, D., Little, J., and O’Shea, D., Ideals, Varieties, and Algorithms. An Introduction to Computational Algebraic Geometry and Commutative Algebra. Second edition. Undergraduate Texts in Mathematics, Springer-Verlag, New York, 1997.Google Scholar
[2] Ding, K., Rook placements and cellular decompositions of partition varieties. Discrete Math. 170(1997), no. 1-3, 107–151.Google Scholar
[3] Ding, K., Rook placements and classification of partition varieties B\M ƛ . Commun. Contemp. Math. 3(2001), no. 4, 495–500.Google Scholar
[4] Foata, D. and Schützenberger, M.-P., On the rook polynomials of Ferrers relations. In: Combinatorial Theory and Its Applications, II. North-Holland, Amsterdam, 1970, pp. 413–436.Google Scholar
[5] Fulton, W., Young tableaux. London Mathematical Society Student Texts 35, Cambridge University Press, Cambridge, 1997.Google Scholar
[6] Garsia, A. M. and Remmel, J. B., Q-counting rook configurations and a formula of Frobenius. J. Combin. Theory Ser. A 41(1986), no. 2, 246–275.Google Scholar
[7] Gasharov, V. and Reiner, V., Cohomology of smooth Schubert varieties in partial flag manifolds. J. London Math. Soc. 66(2002), 550–562.Google Scholar
[8] Goldman, J. R., Joichi, J. T., and White, D. E., Rook theory. I. Rook equivalence of Ferrers boards. Proc. Amer. Math. Soc. 52(1975), 485–492.Google Scholar
[9] Kaplansky, I. and Riordan, J., The problem of the rooks and its applications. Duke Math. J. 13(1946), 259–268.Google Scholar
[10] Macdonald, I. G., Notes on Schubert polynomials. Publications du LACIM, Université du Québec à Montréal, 1991.Google Scholar
[11] Munkres, J. R., Elements of algebraic topology. Addison-Wesley, Menlo Park, CA, 1984.Google Scholar
[12] Springer, T. A., Regular elements of finite reflection groups. Invent. Math. 25(1974), 159–198.Google Scholar