Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-18T22:48:46.107Z Has data issue: false hasContentIssue false
  • English
  • Français

k(n)-Torsion-Free H-Spaces and P(n)-Cohomology

Published online by Cambridge University Press:  20 November 2018

J. Michael Boardman  and
W. Stephen Wilson
J. Michael Boardman
Affiliation:
Department of Mathematics, Johns Hopkins University, 3400 N. Charles St., Baltimore, MD 21218-2689, U.S.A. email: [email protected], [email protected]
W. Stephen Wilson
Affiliation:
Department of Mathematics, Johns Hopkins University, 3400 N. Charles St., Baltimore, MD 21218-2689, U.S.A. email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The $H$-space that represents Brown-Peterson cohomology 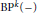$\text{B}{{\text{P}}^{k}}\left( - \right)$ was split by the second author into indecomposable factors, which all have torsion-free homotopy and homology. Here, we do the same for the related spectrum 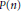$P\left( n \right)$, by constructing idempotent operations in 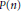$P\left( n \right)$-cohomology 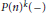$P{{(n)}^{k}}\left( - \right)$ in the style of Boardman-Johnson-Wilson; this relies heavily on the Ravenel-Wilson determination of the relevant Hopf ring. The resulting 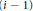$\left( i\,-\,1 \right)$-connected $H$-spaces 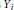${{Y}_{i}}$ have free connective Morava $K$-homology 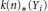$k{{(n)}_{*}}({{Y}_{i}})$, and may be built from the spaces in the 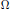$\Omega$-spectrum for 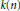$k\left( n \right)$ using only 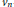${{v}_{n}}$-torsion invariants.

We also extend Quillen's theorem on complex cobordism to show that for any space 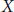$X$, the 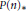$P{{\left( n \right)}_{*}}$-module 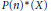$P{{(n)}^{*}}\,(X)$ is generated by elements of 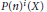$P{{(n)}^{i}}(X)$ for 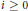$i\,\ge \,0$. This result is essential for the work of Ravenel-Wilson-Yagita, which in many cases allows one to compute BP-cohomology from Morava $K$-theory.

Keywords

55N2255P45
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 6 , 01 December 2007 , pp. 1154 - 1206
Copyright
Copyright © Canadian Mathematical Society 2007

References

[Ad74] Adams, J. F., Stable Homotopy and Generalised Homology. University of Chicago Press, Chicago, 1974.Google Scholar
[Ba73] Baas, N. A., On bordism theory of manifolds with singularities. Math. Scand. 33(1973), 279–302.Google Scholar
[Be86] Bendersky, M., The BP Hopf invariant. Amer. J. Math. 108(1986), no. 5, 1037–1058.Google Scholar
[Bo95] Boardman, J. M., Stable operations in generalized cohomology. In: Handbook of Algebraic Topology. North-Holland, Amsterdam, 1995, pp. 585–686.Google Scholar
[BJW95] Boardman, J. M., Johnson, D. C., and Wilson, W. S., Unstable operations in generalized cohomology. In: Handbook of Algebraic Topology. North-Holland, Amsterdam, 1995, pp. 687–828.Google Scholar
[BW01] Boardman, J. M. and Wilson, W. S., Unstable splittings related to Brown-Peterson cohomology. In: CohomologicalMethods in Homotopy Theory. Progr. Math. 196, Birkhäuser Verlag, Basel, 2001, pp. 35–45.Google Scholar
[Bo] Boardman, J. M., The ring spectra K(n) and P(n) for the prime 2. http://www.math.jhu.edu/∼jmb Google Scholar
[CF66] Conner, P. E. and Floyd, E. E., The relation of cobordism to K-theories. Lecture Notes in Mathematics 28, Springer-Verlag, Berlin, 1966.Google Scholar
[EKMM96] Elmendorf, A. D., Kriz, I., Mandell, M. A., and May, J. P., Rings, Modules and Algebras in Stable Homotopy Theory. Amer. Math. Soc. Mathematical Surveys and Monographs 47, American Mathematical Society, Providence, RI, 1996.Google Scholar
[JW73] Johnson, D. C. and Wilson, W. S., Projective dimension and Brown-Peterson homology. Topology 12(1973), 327–353.Google Scholar
[JW75] Johnson, D. C. and Wilson, W. S., BP operations and Morava's extraordinary K-theories. Math. Z. 144(1975), no. 1, 55–75.Google Scholar
[KW87] Kultze, R. and Würgler, U., A note on the algebra P(n)*(P(n)) for the prime 2 . Manuscripta Math. 57(1987), no. 2, 195–203.Google Scholar
[La76] Landweber, P. S., Homological properties of comodules over MU *(MU) and BP*(BP). Amer. J. Math. 98(1976), no. 3, 591–610.Google Scholar
[Ma71] Mac Lane, S., Categories for the Working Mathematician, Graduate Texts in Mathematics 5, Springer-Verlag, New York, 1971.Google Scholar
[Mi75] Mironov, O. K., Existence of multiplicative structures in the theories of cobordism with singularities. Math. USSR-Izv. 9 (1975), 1007–1034, tr. from Izv. Akad. Nauk SSSR Ser. Mat. 39(1975), 1065–1092.Google Scholar
[Mi78] Mironov, O. K., Multiplications in cobordism theories with singularities, and Steenrod–tom Dieck operations. Math. USSR-Izv. 13(1979), 89–106, tr. from Izv. Akad. Nauk SSSR Ser. Mat. 42(1978), no. 4, 789–806.Google Scholar
[Mo79] Morava, J., A product for the odd-primary bordism of manifolds with singularities. Topology 18(1979), no. 4, 177–186.Google Scholar
[Mo85] Morava, J., Noetherian localisations of categories of cobordism comodules. Ann. of Math. 121(1985), no. 1, 1–39.Google Scholar
[Na02] Nassau, C., On the structure of P(n)*(P(n)) for p = 2. Trans. Amer.Math. Soc. 354(2002), no.5, 1749–1757.Google Scholar
[RW77] Ravenel, D. C. and Wilson, W. S., The Hopf ring for complex cobordism, J. Pure Appl. Algebra 9(1976/77), no. 3, 241–280.Google Scholar
[RW96] Ravenel, D. C. and Wilson, W. S., The Hopf ring for P(n). Canad. J. Math. 48(1996), no. 5, 1044–1063.Google Scholar
[RWY98] Ravenel, D. C., Wilson, W. S., and Yagita, N., Brown-Peterson cohomology from Morava K-theory. K-Theory 15(1998), no. 2, 149–199.Google Scholar
[SY76] Shimada, N. and Yagita, N., Multiplications in the complex bordism theory with singularities. Publ. Research Inst. Math. Sci. 12(1976), no. 1, 259–293.Google Scholar
[St99] Strickland, N. P., Products on MU-modules. Trans. Amer. Math. Soc. 351(1999), no. 7, 2569–2606.Google Scholar
[Wi75] Wilson, W. S., The Ω-spectrum for Brown–Peterson cohomology. II. Amer. J. Math. 97(1975), 101–123.Google Scholar
[Wi84] Wilson, W. S., The Hopf ring for Morava K-theory. Publ. Res. Inst. Math. Sci. 20(1984), no. 5, 1025–1036.Google Scholar
[Wü77] Würgler, U., On products in a family of cohomology theories associated to the invariant prime ideals of π*(BP). Comment. Math. Helv. 52(1977), no. 4, 457–481.Google Scholar
[Ya76] Yagita, N., The exact functor theorem for BP*/In-theory. Proc. Japan Acad. 52(1976), no. 1, 1–3.Google Scholar
[Ya77] Yagita, N., On the algebraic structure of cobordism operations with singularities. J. London Math. Soc. 16(1977), no. 1, 131–141.Google Scholar
[Ya84] Yagita, N., On relations between Brown–Peterson cohomology and the ordinary mod p cohomology theory. Kodai Math. J. 7(1984), no. 2, 273–285.Google Scholar
[Yo76] Yosimura, Z., Projective dimension of Brown–Peterson homology with modul. (p, v 1, … , v n–1) coefficients. Osaka J. Math. 13(1976), no. 2, 289–309.Google Scholar