L. Fuchs states in his book “Infinite Abelian Groups” [6, Vol. I, p. 134] the following

Problem 13. Find conditions on a subgroup of A to be the intersection of a finite number of pure (p-pure) subgroups of A.

The answer to this problem will be given as a special case of our theorem below. In order to find a better setting of this problem recall that a subgroup S ⊆ E is p-pure if pnE ∩ S = pnS for all natural numbers. Then S is pure in E if S is p-pure for all primes p. This generalizes to pσ-isotype, a definition due to L. J. Kulikov, cf. [6, Vol. II, p. 75] and [11, pp. 61, 62]. If α is an ordinal, then S is pσ-isotype if

Soit Ω un domaine borné de RN, et soit f:Ω × R → R une fonction satisfaisant à la condition de Carathéodory (i.e., f(s, ·) est continue pour presque tout s ∊ Ω, et f (·, u) est mesurable pour tout u ∊ R). Considérons l'opérateur de la superposition

(1.1)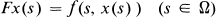

(encore appelé opérateur de Nemyckii), engendré par la fonction f. Cet opérateur joue un grand rôle dans la théorie des équations intégrales, différentielles (ordinaires et aux dérivées partielles), et fonctionnelles-différentielles, où il est important de connaître les propriétés analytiques et topologiques de F dans certains espaces de fonctions mesurables, intégrables, continues, différentiables, analytiques etc., les propriétés les plus importantes étant : théorèmes de transfert, de continuité, de bornage, et de compacité. Par exemple, on connaît de nombreux résultats sur l'opérateur (1) dans les espaces de Lebesgue L (voir [10] pour une présentation assez complète); en effet, si l'opérateur (1) envoie une partie de L , d'intérieur non vide, dans L, alors, il est automatiquement continu et borné sur chaque boule.

1. Introduction. In 1931, Newman [9] showed that a connected manifold cannot accept arbitrarily small period-n homeomorphisms, for any n > 1. In this paper we are concerned with the existence of chainable continua with arbitrarily small homeomorphisms.

For a long time the only known periodic homeomorphisms of chainable continua had periods 1, 2 or 4 [4]. Recently, Wayne Lewis [8] showed that the pseudo-arc admits periodic homeomorphisms of every order, as well as p-adic cantor group actions. We will see that such homeomorphisms can be made arbitrarily small.

In Section 4, a different chainable indecomposable continuum accepting arbitrarily small period-2 homeomorphisms is constructed.

Let X be a quasi-Banach space whose dual X* separates the points of X. Then X* is a Banach space under the norm

From X we can construct the Banach envelope Xc of X by defining for x ∊ X, the norm

Then Xc is the completion of (X, ‖ ‖c). Alternatively ‖ ‖c is the Minkowski functional of the convex hull of the unit ball. Xc has the property that any bounded linear operator L:X → Z into a Banach space extends with preservation of norm to an operator .

In the sequel, πn will denote the class of real polynomials of degree at most n and ‖f(x)‖∞ the L∞-norm of a function on [–l, +1].

In a series of recent papers, Saff and Varga studied the properties of the so-called incomplete polynomials; that is to say polynomials of the form

where sl and s2 are fixed integers and q ∊ πn.

In there, they define the constrained Tchebychev polynomial as being, up to a multiplicative constant, the solution of the following minimization problem

A compact bordered Klein surface of (algebraic) genus g ≦ 2 is said to have maximal symmetry [5] if its automorphism group is of order 12(g – 1), the largest possible. An M*-group acts as the automorphism group of a bordered surface with maximal symmetry. M*-groups were first studied in [6], and additional results about these groups are in [5, 7, 8].

Here we construct a new, interesting family of M*-groups. Each group G in the family is an extension of a cyclic group by the automorphism group of a torus T with holes that has maximal symmetry. Furthermore, G acts on a bordered Klein surface X that is a fully wound covering [7] of T, that is, an especially nice covering in which X has the same number of boundary components as T. The construction we use for the new family of M*-groups is a standard one that employs group automorphisms to define extensions of groups.

1. Introduction. The character theory of solvable groups has undergone significant development during the last decade or so and it can now be seen to have quite a rich structure. In particular, there is an interesting interaction between characters and sets of prime numbers.

Let G be solvable and let π be a set of primes. The “π-special” characters of G are certain irreducible complex characters (defined by D. Gajendragadkar [1]) which enjoy some remarkable properties, many of which were proved in [1]. (We shall review the definition and relevant facts in Section 3 of this paper.) Actually, we need not assume solvability: that G is π-separable is sufficient, if we are willing to use the Feit-Thompson “odd order” theorem occasionally. We shall state and prove our results under this weaker hypothesis, but we stress that anything of interest in them is already interesting in the solvable case where, of course, the “odd order” theorem is irrelevant.

In classical two-valued logic there is a three way relationship among formal systems, Boolean algebras and set theory. In the case of infinite-valued logic we have a similar relationship among formal systems, MV-algebras and what is called Bold fuzzy set theory. The relationship, in the latter case, between formal systems and MV-algebras has been known for many years while the relationship between MV-algebras and fuzzy set theory has hardly been studied. This is not surprising. MV-algebras were invented by C. C. Chang [1] in order to provide an algebraic proof of the completeness theorem of the infinitevalued logic of Lukasiewicz and Tarski. Having served this purpose (see [2]), the study of these algebras has been minimal, see for example [6], [7]. Fuzzy set theory was also being born around the same time and only in recent years has its connection with infinite-valued logic been made, see e.g. [3], [4], [5]. It seems appropriate then, to take a further look at the structure of MV-algebras and their relation to fuzzy set theory.

The Fourier transform of the surface measure on the unit sphere in Rn + 1, as is well-known, equals the Bessel function

Its behaviour at infinity is described by an asymptotic expansion

The purpose of this paper is to obtain such an expression for surfaces Σ other than the unit sphere. If the surface Σ is a sufficiently smooth compact n-surface in Rn + 1 with strictly positive Gaussian curvature everywhere then with only minor changes in the main term, such an asymptotic expansion exists. This result was proved by E. Hlawka in [3]. A similar result concerned with the minimal smoothness of Σ was later obtained by C. Herz [2].

Let D be the open unit disk and let ∂D be its boundary. We denote by C the algebra of continuous functions on ∂d, and by L∞ the algebra of essentially bounded measurable functions with respect to the normalized Lebesgue measure m on ∂D. Let H∞ be the algebra of bounded analytic functions on D. Identifying with their boundary functions, we regard H∞ as a closed subalgebra of L∞. Let A = H∞ Pi C, which is called the disk algebra. The algebras A and H∞ have been studied extensively [5, 6, 7]. In these fifteen years, norm closed subalgebras between H∞ and L∞, called Douglas algebras, have received considerable attention in connection with Toeplitz operators [12]. A norm closed subalgebra between A and H∞ is called an analytic subalgebra. In [2], Dawson studied analytic subalgebras and he remarked that there are many different types of analytic subalgebras. One problem is to study which analytic subalgebras are backward shift invariant. Here, a subset E of H∞ is called backward shift invariant if

In 1911, Schur published a rather formidable paper [9] in which he determined all the complex projective characters for the symmetric group (denoted Σn here, despite the title), and for the alternating group An (A pronounced “alpha”). As far as we know, the construction of the modules involved is still an unsolved problem. The results of Schur can be expressed in terms of certain induced representations whose characters form a basis for the group of virtual characters, plus formulae expressing the irreducible characters in terms of these induced characters. Here we give a new formulation of the above induced characters in the spirit of the well known “induction algebra” approach to the linear representations of Σn. We use some Hopf algebra techniques inspired by [5] to give new proofs of Schur's results, and to determine the extra structure which we define.

It is at present well known that, if q(x, t) is a solution of the Korteweg de Vries (K d V) equation

(1)

such that q(x, 0) = q0(x), where q0(x) behaves reasonably at infinity, and if

are the scattering data (see [4]) corresponding to q(x, t), then

Let L be a very ample line bundle on a smooth, connected, projective, ruled not rational surface X. We have considered the problem of classifying biholomorphically smooth, connected, projected, ruled, non rational surfaces X with smooth hyperplane section C such that the genus g = g(C) is less than or equal to six and dim where is the map associated to . L. Roth in [10] had given a birational classification of such surfaces. If g = 0 or 1 then X has been classified, see [8].

If g = 2 ≠ hl,0(X) by [12, Lemma (2.2.2) ] it follows that X is a rational surface. Thus we can assume g ≦ 3.

Since X is ruled, h2,0(X) = 0 and

see [4] and [12, p. 390].

Let a and n be positive integers such that f(x) = xn + a is irreducible over the integers. A conjecture made by Bouniakowsky [4] in 1857 would imply that there exist infinitely many integers x such that f(x) is prime. An even stronger conjecture of Bateman and Horn [1, 2] would imply that

where π(x;f) is the number of integers m with 0 ≧ m ≧ x for which f(m) is prime, and

where w(p) is the number of solutions of the congruence

Except for the trivial case n = 1, neither of these conjectures has ever been resolved.

Let A be a C*-algebra, B a C*-subalgebra of A, δ:B → A a derivation, i.e., a linear map with

There has been considerable interest for several years now in the question of when δ can be extended from B to a derivation of A (see, for example, [8], Section 4, [1], [5], [4], [6], [9], [10], [11]). The paper before the reader will be concerned with this extension problem when B is a hereditary C*-subalgebra of A.

Our work takes its cue from the paper [6] of George Elliott. We prove in Section 2 of the present paper that derivations as described above of a unital hereditary C*-subalgebra always extend whenever A is either simple, AW*, separable and AF, or separable with continuous trace, thus generalizing and extending Theorem 4.5 of [6].

1. Introduction. One of the most remarkable q-extensions of the classical beta integral was recently introduced by Askey and Wilson [1]

(1.1)

where |q| < 1 and the pairwise products of {a, b, c, d} as a multiset do not belong to the set {qj, j = 0, – 1, – 2, …}. The contour C is the unit circle described in the positive direction, but with suitable deformations to separate the sequences of poles converging to zero from the sequences of poles diverging to infinity. The symbol (A; q)∞ is an infinite product defined by

(1.2)

whenever it converges.

A collection of matrices over a field F is said to be triangularizable if there is an invertible matrix T over F such that the matrices T−1ST, are all upper triangular. It is a well-known and easy fact that any commutative set is triangularizable if F is algebraically closed, or if F contains the spectrum of every member of . Many sufficient conditions are known for triangularizability of matrix collections. Levitzki [7] proved that a (multiplicative) semigroup of nilpotent matrices is triangularizable. (His result is valid even over a division ring.) Kolchin [5] showed the triangularizability of a semigroup of unipotent matrices, i.e., matrices of the form I + N with N nilpotent. Kaplansky [3, 4] unified and generalized these results.

Soient Lp(X, , μ) les espaces de Banach usuels associés à un espace mesuré fini ou α-fini (X, , μ), p étant un nombre réel compris entre un et l'infini (1 < p < ∞). Notons Lp, l'espace Lp[0, 1]. Un opérateur T:Lp → Lp est dit être à puissances bornées sur Lp si

La convergence presque sure de la suite de fonctions

a été étudiée dans L2 pour T contraction [8], [1] et pour T inversible à puissances bornées dans , 1 < p ≧ 2 [9].

Given a lattice L and a convex sublattice K of L, it is well-known that the map Con L → Con K from the congruence lattice of L to that of K determined by restriction is a lattice homomorphism preserving 0 and 1. It is a classical result (first discovered by R. P. Dilworth, unpublished, then by G. Grätzer and E. T. Schmidt [2], see also [1], Theorem II.3.17, p. 81) that any finite distributive lattice is isomorphic to the congruence lattice of some finite lattice. Although it has been conjectured that any algebraic distributive lattice is the congruence lattice of some lattice, this has not yet been proved in its full generality. The best result is in [4]. The conjecture is true for ideal lattices of lattices with 0; see also [3].

Soit Ω un domaine de Jordan à bord rectifiable du plan complexe C. Désignons par dλ la mesure de Lebesgue à l'intérieur de Ω, par dσ la mesure de Lebesgue sur le bord ∂Ω de Ω et par φ une représentation conforme de Ω sur le disque unité D du plan complexe.

Par définition, la classe de Bergman Ap(Ω), 0 < p ≦ +∞, est le sous-espace de Lp(dλ) formé par les fonctions holomorphes dans Ω et le projecteur de Bergman PΩ de Ω est le projecteur orthogonal de L2(dλ) sur A2(Ω); quel que soit f dans L2(dλ), on a la formule:

(1)