Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T06:11:33.624Z Has data issue: false hasContentIssue false
  • English
  • Français

A Trace Condition Equivalent to Simultaneous Triangularizability

Published online by Cambridge University Press:  20 November 2018

Heydar Radjavi
Heydar Radjavi*
Affiliation:
Dalhousie University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

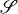A collection of matrices over a field F is said to be triangularizable if there is an invertible matrix T over F such that the matrices T−1ST, 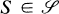are all upper triangular. It is a well-known and easy fact that any commutative set 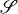is triangularizable if F is algebraically closed, or if F contains the spectrum of every member of 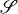. Many sufficient conditions are known for triangularizability of matrix collections. Levitzki [7] proved that a (multiplicative) semigroup of nilpotent matrices is triangularizable. (His result is valid even over a division ring.) Kolchin [5] showed the triangularizability of a semigroup of unipotent matrices, i.e., matrices of the form I + N with N nilpotent. Kaplansky [3, 4] unified and generalized these results.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 2 , 01 April 1986 , pp. 376 - 386
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Dunford, N. and Schwartz, J. T., Linear operators, Part II: Spectral theory (Interscience, New York, 1963).Google Scholar
2. Jacobson, N., Lectures in abstract algebra II: linear algebra (van Nostrand, Princeton, 1953).CrossRefGoogle Scholar
3. Kaplansky, I., Fields and rings, 2nd Ed. (University of Chicago Press, Chicago, 1972).Google Scholar
4. Kaplansky, I., The Engel-Kolchin theorem revisited, in Contributions to algebra (Academic Press, New York, 1977).Google Scholar
5. Kolchin, E., On certain concepts in the theory of algebraic matric groups, Ann. of Math. 49 (1948), 774–789.Google Scholar
6. Laurie, C., Nordgren, E., Radjavi, H. and Rosenthal, P., On triangularization of algebras of operators, J. Reine Angew. Math. 327 (1981), 143–155.Google Scholar
7. Levitzki, J., Uber nilpotente Unterringe, Math. Ann. 105 (1931), 620–627.Google Scholar
8. Lomonosov, V. J., Invariant subspaces for operators commuting with compact operators, Funkcional Anal, i Prilozen 7 (1973), (Russian); Functional Anal. Appl. 7 (1973), 213–214.Google Scholar
9. McCoy, N. H., On the characteristic roots of matric polynomials, Bull. Amer. Math. Soc. 42 (1936), 592–600.Google Scholar
10. Nordgren, E., Radjavi, H. and Rosenthal, P., Triangularizing semigroups of compact operators, Indiana Univ. Math. J. 33 (1984), 271–275.Google Scholar
11. Radjavi, H., Isomorphisms of transitive operator algebras, Duke Math. J. 41 (1974), 555–564.Google Scholar
12. Radjavi, H., On the reduction and triangularization of semigroups of operators, J. Operator Theory 13 (1985), 63–71.Google Scholar
13. Radjavi, H. and Rosenthal, P., On transitive and reductive operator algebras, Math. Ann. 209 (1974), 43–56.Google Scholar
14. Radjavi, H. and Rosenthal, P., Invariant subspaces (Springer-Verlag, New York, 1973).CrossRefGoogle Scholar
16. Ringrose, J. R., Compact non-self adjoint operators (Van Nostrand, Princeton, 1971).Google Scholar
17. Watters, J. F., Block triangularization of algebras of matrices, Linear Alg. App. 32 (1980), 3–7 Google Scholar