Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Martín-Reyes, F. J.
and
De la Torre, A.
1988.
The dominated ergodic estimate for mean bounded, invertible, positive operators.
Proceedings of the American Mathematical Society,
Vol. 104,
Issue. 1,
p.
69.
Гапошкин, Владимир Федорович
and
Gaposhkin, Vladimir Fedorovich
2000.
О максимальной квадратичной функции для степенно-ограниченных операторов в $L^p$.
Математические заметки,
Vol. 67,
Issue. 6,
p.
950.
Yahdi, M.
2006.
Super-Ergodic operators.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 9,
p.
2613.
Tempelman, A.
2015.
Pointwise ergodic theorems for bounded Lamperti representations of amenable groups.
Proceedings of the American Mathematical Society,
Vol. 143,
Issue. 11,
p.
4989.
Cohen, Guy
2018.
Doubly power-bounded operators on L, 2 ≠ p > 1.
Journal of Mathematical Analysis and Applications,
Vol. 466,
Issue. 2,
p.
1327.
Tempelman, Arkady
and
Shulman, Alexander
2019.
Dominated and pointwise ergodic theorems with “weighted” averages for bounded Lamperti representations of amenable groups.
Journal of Mathematical Analysis and Applications,
Vol. 474,
Issue. 1,
p.
23.
Bermúdez, Teresa
Bonilla, Antonio
Müller, Vladimír
and
Peris, Alfredo
2020.
Cesàro bounded operators in Banach spaces.
Journal d'Analyse Mathématique,
Vol. 140,
Issue. 1,
p.
187.
Cohen, Guy
Cuny, Christophe
Eisner, Tanja
and
Lin, Michael
2020.
Resolvent conditions and growth of powers of operators.
Journal of Mathematical Analysis and Applications,
Vol. 487,
Issue. 2,
p.
124035.
Akrym, Abdellah
El Bakkali, Abdeslam
and
Faouzi, Abdelkhalek
2023.
ON THE LOCAL KREISS RESOLVENT CONDITION.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 2,


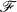 ,
, 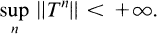
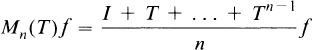
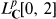 , 1 <
, 1 < 