No CrossRef data available.
Article contents
Continuity of the Scattering Transformation for the Korteweg de Vries Equation
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
It is at present well known that, if q(x, t) is a solution of the Korteweg de Vries (K d V) equation
(1)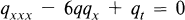
such that q(x, 0) = q0(x), where q0(x) behaves reasonably at infinity, and if

are the scattering data (see [4]) corresponding to q(x, t), then

- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1986
References
1.
Ablowitz, M. J. and Segur, H., Solitons and the inverse scattering transform,
SIAM (1981).CrossRefGoogle Scholar
2.
Chadan, K. and Sabatier, P. C., Inverse problems in quantum scattering theory (Springer Verlag, 1977).CrossRefGoogle Scholar
3.
Deift, P. and Trubowitz, E., Inverse scattering on the line,
Comm. on pure and appl. Math.
32 (1979), 121.Google Scholar
4.
Faddeev, L. D., Properties of the S-matrix of the one-dimensional Schroëdinger equation,
Trusdy, mat. inst., Steklov
73 (1964), 314.Google Scholar
5.
Montel, P., Leçons sur les familles normales de fonctions analytiques et leurs applications (Chelsea publishing company, New York, 1974).Google Scholar
6.
Saks, S. and Zygmund, A., Analytic functions (Paristwewe Widawniscto Nankowe, Warsave, 1965).Google Scholar


