This paper is concerned with the residual spectrum of the hermitian quaternionic classical groups $G_{n}^{\prime }$ and $H_{n}^{\prime }$ defined as algebraic groups for a quaternion algebra over an algebraic number field. Groups $G_{n}^{\prime }$ and $H_{n}^{\prime }$ are not quasi-split. They are inner forms of the split groups $\text{S}{{\text{O}}_{4n}}$ and $\text{S}{{\text{p}}_{4n}}$. Hence, the parts of the residual spectrum of $G_{n}^{\prime }$ and $H_{n}^{\prime }$ obtained in this paper are compared to the corresponding parts for the split groups $\text{S}{{\text{O}}_{4n}}$ and $\text{S}{{\text{p}}_{4n}}$.

Let $R$ be a homomorphic image of a Gorenstein local ring. Recent work has shown that there is a bridge between Auslander categories and modules of finite Gorenstein homological dimensions over $R$.

We use Gorenstein dimensions to prove new results about Auslander categories and vice versa. For example, we establish base change relations between the Auslander categories of the source and target rings of a homomorphism $\varphi :\,R\,\to \,S$ of finite flat dimension.

A set in a metric space is called a Čebyšev set if it has a unique “nearest neighbour” to each point of the space. In this paper we generalize this notion, defining a set to be Čebyšev relative to another set if every point in the second set has a unique “nearest neighbour” in the first. We are interested in Čebyšev sets in some hyperspaces over ${{\text{R}}^{n}}$, endowed with the Hausdorff metric, mainly the hyperspaces of compact sets, compact convex sets, and strictly convex compact sets.

We present some new classes of Čebyšev and relatively Čebyšev sets in various hyperspaces. In particular, we show that certain nested families of sets are Čebyšev. As these families are characterized purely in terms of containment,without reference to the semi-linear structure of the underlyingmetric space, their properties differ markedly from those of known Čebyšev sets.

We introduce a new approach to an enumerative problem closely linked with the geometry of branched coverings, that is, we study the number ${{H}_{\alpha }}({{i}_{2}},{{i}_{3}},...)$ of ways a given permutation (with cycles described by the partition $\alpha $) can be decomposed into a product of exactly ${{i}_{2}}$ 2-cycles, ${{i}_{3}}$ 3-cycles, etc., with certain minimality and transitivity conditions imposed on the factors. The method is to encode such factorizations as planar maps with certain descent structure and apply a new combinatorial decomposition to make their enumeration more manageable. We apply our technique to determine ${{H}_{\alpha }}({{i}_{2}},{{i}_{3}},...)$ when $\alpha $ has one or two parts, extending earlier work of Goulden and Jackson. We also show how these methods are readily modified to count inequivalent factorizations, where equivalence is defined by permitting commutations of adjacent disjoint factors. Our technique permits us to generalize recent work of Goulden, Jackson, and Latour, while allowing for a considerable simplification of their analysis.

We study the effect of two types of degeneration of a Riemannian metric on the first eigenvalue of the Laplace operator on surfaces. In both cases we prove that the first eigenvalue of the round sphere is an optimal asymptotic upper bound. The first type of degeneration is concentration of the density to a point within a conformal class. The second is degeneration of the conformal class to the boundary of the moduli space on the torus and on the Klein bottle. In the latter, we follow the outline proposed by N. Nadirashvili in 1996.

Let $\Xi $ be a discrete set in ${{\mathbb{R}}^{d}}$. Call the elements of $\Xi $centers. The well-known Voronoi tessellation partitions ${{\mathbb{R}}^{d}}$ into polyhedral regions (of varying volumes) by allocating each site of ${{\mathbb{R}}^{d}}$ to the closest center. Here we study allocations of ${{\mathbb{R}}^{d}}$ to $\Xi $ in which each center attempts to claim a region of equal volume $\alpha $.

We focus on the case where $\Xi $ arises from a Poisson process of unit intensity. In an earlier paper by the authors it was proved that there is a unique allocation which is stable in the sense of the Gale–Shapley marriage problem. We study the distance $X$ from a typical site to its allocated center in the stable allocation.

The model exhibits a phase transition in the appetite $\alpha $. In the critical case $\alpha \,=\,1$ we prove a power law upper bound on $X$ in dimension $d\,=\,1$. (Power law lower bounds were proved earlier for all $d$). In the non-critical cases $\alpha <1$ and $\alpha \,>1$we prove exponential upper bounds on $X$.

In this article we study injective representations of infinite quivers. We classify the indecomposable injective representations of trees and describe Gorenstein injective and projective representations of barren trees.

We produce ample (resp. NEF, eventually free) divisors in the Kontsevich space ${{\overline{\mathcal{M}}}_{\text{0,}n}}\left( {{\mathbb{P}}^{r}},d \right)$ of $n$-pointed, genus 0, stable maps to ${{\mathbb{P}}^{r}}$, given such divisors in ${{\overline{\mathcal{M}}}_{\text{0,}n+d}}$ We prove that this produces all ample (resp. NEF, eventually free) divisors in ${{\overline{\mathcal{M}}}_{\text{0,}n}}\left( {{\mathbb{P}}^{r}},\,d \right)$ As a consequence, we construct a contraction of the boundary $\,\,\mathop{\bigcup }_{k=1}^{\left\lfloor {d}/{2}\; \right\rfloor }\,{{\Delta }_{k,d-k}}$ in ${{\overline{\mathcal{M}}}_{\text{0,}0}}\left( {{\mathbb{P}}^{r}},d \right)$ analogous to a contraction of the boundary $\mathop{\bigcup }_{k=3}^{\left\lfloor {n}/{2}\; \right\rfloor }\,{{\widetilde{\Delta }}_{k,n-k}}$ in ${{\overline{\mathcal{M}}}_{\text{0,}n}}$ first constructed by Keel and McKernan.

Pour toute sous-vari ét é géométriquement irréductible $V$ du groupe multiplicatif $\mathbb{G}_{m}^{n}$, on sait qu’en dehors d’un nombre fini de translat és de tores exceptionnels inclus dans $V$, tous les points sont de hauteur minorée par une certaine quantité $q{{(V)}^{-1}}>0$. On connaît de plus une borne supérieure pour la somme des degrés de ces translatés de tores pour des valeurs de $q(V)$ polynomiales en le degré de $V$. Ceci n’est pas le cas si l’on exige une minoration quasi-optimale pour la hauteur des points de $V$, essentiellement linéaire en l’inverse du degré.

Nous apportons ici une réponse partielle à ce problème : nous donnons une majoration de la somme des degrés de ces translat és de sous-tores de codimension 1 d’une hypersurface $V$. Les résultats, obtenus dans le cas de $\mathbb{G}_{m}^{3}$,mais complètement explicites, peuvent toutefois s’étendre à $\mathbb{G}_{m}^{n}$,moyennant quelques petites complications inhérentes à la dimension $n$.

We prove the ${{L}^{P}}({{\mathbb{R}}^{d}})(1<p\le \infty )$ boundedness of the maximal operators associated with a family of vector polynomials given by the form $\left\{ ({{2}^{{{k}_{1}}}}{{\mathfrak{p}}_{1}}(t),...,{{2}^{{{k}_{d}}}}{{\mathfrak{p}}_{d}}(t)):t\in \mathbb{R} \right\}$. Furthermore, by using the lifting argument, we extend this result to a general class of vector polynomials whose coefficients are of the form constant times ${{2}^{k}}$.

For every polytope $\mathcal{P}$ there is the universal regular polytope of the same rank as $\mathcal{P}$ corresponding to the Coxeter group $\mathcal{C}\,=\,\left[ \infty ,\,.\,.\,.\,,\,\infty \right]$. For a given automorphism $d$ of $\mathcal{C}$, using monodromy groups, we construct a combinatorial structure ${{P}^{d}}$. When ${{P}^{d}}$ is a polytope isomorphic to $\mathcal{P}$ we say that $\mathcal{P}$ is self-invariant with respect to $d$, or $d$-invariant. We develop algebraic tools for investigating these operations on polytopes, and in particular give a criterion on the existence of a $d$-automorphism of a given order. As an application, we analyze properties of self-dual edge-transitive polyhedra and polyhedra with two flag-orbits. We investigate properties of medials of such polyhedra. Furthermore, we give an example of a self-dual equivelar polyhedron which contains no polarity (duality of order 2). We also extend the concept of Petrie dual to higher dimensions, and we show how it can be dealt with using self-invariance.

The space now known as complete Erdős space${{\mathfrak{E}}_{\text{c}}}$ was introduced by Paul Erdős in 1940 as the closed subspace of the Hilbert space ${{\ell }^{2}}$ consisting of all vectors such that every coordinate is in the convergent sequence $\left\{ 0 \right\}\cup \left\{ 1/n:n\in \mathbb{N}\ \right\}$. In a solution to a problem posed by Lex $G$. Oversteegen we present simple and useful topological characterizations of ${{\mathfrak{E}}_{\text{c}}}$. As an application we determine the class of factors of ${{\mathfrak{E}}_{\text{c}}}$. In another application we determine precisely which of the spaces that can be constructed in the Banach spaces ${{\ell }^{p}}$ according to the ‘Erdős method’ are homeomorphic to ${{\mathfrak{E}}_{\text{c}}}$. A novel application states that if $I$ is a Polishable ${{F}_{\sigma }}$-ideal on $\omega $, then $I$ with the Polish topology is homeomorphic to either $\mathbb{Z}$, the Cantor set ${{2}^{\omega }},\,\mathbb{Z}\,\times \,{{2}^{\omega }}$, or ${{\mathfrak{E}}_{\text{c}}}$. This last result answers a question that was asked by Stevo Todorčević.

In this paper we study the notion of a convex subordination chain in several complex variables. We obtain certain necessary and sufficient conditions for a mapping to be a convex subordination chain, and we give various examples of convex subordination chains on the Euclidean unit ball in ${{\mathbb{C}}^{n}}$. We also obtain a sufficient condition for injectivity of $f(z/\|z\|,\,\,\|z\|)$ on ${{B}^{n}}\backslash \{0\}$, where $f(z,t)$ is a convex subordination chain over $(0,1)$.

Let $\lambda $ be a fixed integer exceeding 1 and ${{s}_{n}}$ any strictly increasing sequence of positive integers satisfying ${{s}_{n}}\le {{n}^{15/14+o(1)}}$. In this paper we give a version of the large sieve inequality for the sequence ${{\lambda }^{{{s}_{n}}}}$. In particular, we obtain nontrivial estimates of the associated trigonometric sums “on average” and establish equidistribution properties of the numbers ${{\lambda }^{{{s}_{n}}}},n\le p{{(\log p)}^{2+\varepsilon }}$, modulo $p$ for most primes $p$.

We construct covering maps from infinite blowups of the $n$-dimensional Sierpinski gasket $S{{G}_{n}}$ to certain compact fractafolds based on $S{{G}_{n}}$. These maps are fractal analogs of the usual covering maps fromthe line to the circle. The construction extends work of the second author in the case $n=2$, but a differentmethod of proof is needed, which amounts to solving a Sudoku-type puzzle. We can use the covering maps to define the notion of periodic function on the blowups. We give a characterization of these periodic functions and describe the analog of Fourier series expansions. We study covering maps onto quotient fractalfolds. Finally, we show that such covering maps fail to exist for many other highly symmetric fractals.

The theorems of Gross–Zagier and Zhang relate the Néron–Tate heights of complex multiplication points on the modular curve ${{X}_{0}}\,(N)$ (and on Shimura curve analogues) with the central derivatives of automorphic $L$-function. We extend these results to include certain CM points on modular curves of the form $X({{\Gamma }_{0}}(M)\bigcap {{\Gamma }_{1}}(S))$ (and on Shimura curve analogues). These results are motivated by applications to Hida theory that can be found in the companion article “Central derivatives of $L$ -functions in Hida families”, Math. Ann. 399(2007), 803–818.

We study the algebraic properties of Generalized Laguerre Polynomials for negative integral values of the parameter. For integers $r,n\ge 0$, we conjecture that $L_{n}^{(-1-n-r)}(x)=\Sigma _{j=0}^{n}\left( _{n-j}^{n-j+r} \right){{x}^{j}}/j!$ is a $\mathbb{Q}$-irreducible polynomial whose Galois group contains the alternating group on $n$ letters. That this is so for $r=n$ was conjectured in the 1950's by Grosswald and proven recently by Filaseta and Trifonov. It follows fromrecent work of Hajir and Wong that the conjecture is true when $r$ is large with respect to $n\ge 5$. Here we verify it in three situations: (i) when $n$ is large with respect to $r$, (ii) when $r\le 8$, and (iii) when $n\le 4$. The main tool is the theory of $p$-adic Newton Polygons.

The multiplicity conjecture of Herzog, Huneke, and Srinivasan is verified for the face rings of the following classes of simplicial complexes: matroid complexes, complexes of dimension one and two, and Gorenstein complexes of dimension at most four. The lower bound part of this conjecture is also established for the face rings of all doubly Cohen–Macaulay complexes whose 1-skeleton's connectivity does not exceed the codimension plus one as well as for all $\text{(}d-1)$-dimensional $d$-Cohen–Macaulay complexes. The main ingredient of the proofs is a new interpretation of the minimal shifts in the resolution of the face ring $\mathbf{k}[\Delta ]$ via the Cohen–Macaulay connectivity of the skeletons of $\Delta $.

Let 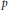$p$ be a prime, and let 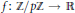$f:\mathbb{Z}/p\mathbb{Z}\to \mathbb{R}$ be a function with 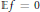$\mathbb{E}f=0$ and 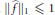$||\hat{f}|{{|}_{1}}\le 1$. Then 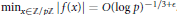${{\min }_{x\in \mathbb{Z}/p\mathbb{Z}}}|f\left( x \right)|=O{{\left( \log p \right)}^{-1/3+\in }}$. One should think of 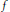$f$ as being “approximately continuous”; our result is then an “approximate intermediate value theorem”.

As an immediate consequence we show that if 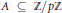$A\subseteq \mathbb{Z}/p\mathbb{Z}$ is a set of cardinality 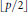$\left\lfloor {p}/{2}\; \right\rfloor $, then 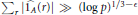${{\sum }_{r}}\widehat{|\,{{1}_{A}}}\left( r \right)|\gg {{\left( \log p \right)}^{1/3-\in }}$. This gives a result on a “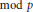$\,\bmod \,p$” analogue of Littlewood's well-known problem concerning the smallest possible 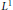${{L}^{1}}$-norm of the Fourier transform of a set of $n$ integers.

Another application is to answer a question of Gowers. If 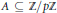$A\,\subseteq \,{\mathbb{Z}}/{p\mathbb{Z}}\;$ is a set of size 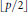$\left\lfloor {p}/{2}\; \right\rfloor $, then there is some 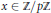$x\,\in \,\mathbb{Z}/p\mathbb{Z}$ such that

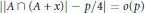$$||A\cap \left( A+x \right)\,-\,p/4|\,=o\left( p \right).$$

Let $K$ be a complex reductive algebraic group and $V$ a representation of $K$. Let $S$ denote the ring of polynomials on $V$. Assume that the action of $K$ on $S$ is multiplicity-free. If $\lambda $ denotes the isomorphism class of an irreducible representation of $K$, let $\rho \lambda :K\to GL({{V}_{\lambda }})$ denote the corresponding irreducible representation and ${{S}_{\lambda }}$ the $\lambda $-isotypic component of $S$. Write ${{S}_{\lambda }}.{{S}_{\mu }}$ for the subspace of $S$ spanned by products of ${{S}_{\lambda }}$ and ${{S}_{\mu }}$. If ${{V}_{v}}$ occurs as an irreducible constituent of ${{V}_{\lambda }}\otimes {{V}_{\mu }}$, is it true that ${{S}_{v}}\subseteq {{S}_{\lambda }}.{{S}_{\mu }}?$ In this paper, the authors investigate this question for representations arising in the context of Hermitian symmetric pairs. It is shown that the answer is yes in some cases and, using an earlier result of Ruitenburg, that in the remaining classical cases, the answer is yes provided that a conjecture of Stanley on the multiplication of Jack polynomials is true. It is also shown how the conjecture connects multiplication in the ring $S$ to the usual Littlewood–Richardson rule.