Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-18T13:10:28.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplication of Polynomials on Hermitian Symmetric spaces and Littlewood–Richardson Coefficients

Published online by Cambridge University Press:  20 November 2018

William Graham  and
Markus Hunziker
William Graham
Affiliation:
Department of Mathematics, The University of Georgia, Athens, GA 30602-7403, USA, [email protected]
Markus Hunziker
Affiliation:
Department of Mathematics, The University of Georgia, Athens, GA 30602-7403, USA, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 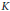$K$ be a complex reductive algebraic group and 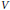$V$ a representation of 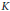$K$. Let 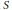$S$ denote the ring of polynomials on 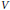$V$. Assume that the action of 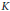$K$ on 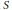$S$ is multiplicity-free. If 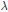$\lambda $ denotes the isomorphism class of an irreducible representation of 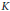$K$, let 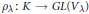$\rho \lambda :K\to GL({{V}_{\lambda }})$ denote the corresponding irreducible representation and 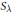${{S}_{\lambda }}$ the 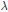$\lambda $-isotypic component of 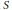$S$. Write 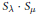${{S}_{\lambda }}.{{S}_{\mu }}$ for the subspace of 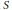$S$ spanned by products of 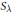${{S}_{\lambda }}$ and 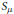${{S}_{\mu }}$. If 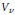${{V}_{v}}$ occurs as an irreducible constituent of 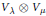${{V}_{\lambda }}\otimes {{V}_{\mu }}$, is it true that 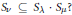${{S}_{v}}\subseteq {{S}_{\lambda }}.{{S}_{\mu }}?$ In this paper, the authors investigate this question for representations arising in the context of Hermitian symmetric pairs. It is shown that the answer is yes in some cases and, using an earlier result of Ruitenburg, that in the remaining classical cases, the answer is yes provided that a conjecture of Stanley on the multiplication of Jack polynomials is true. It is also shown how the conjecture connects multiplication in the ring 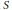$S$ to the usual Littlewood–Richardson rule.

Keywords

14L3022E46Hermitian symmetric spacesmultiplicity free actionsLittlewood–Richardson coefficientsJack polynomials
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 351 - 372
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Alexeev, V. and Brion, M., Stable reductive varieties. I. Affine varieties. Invent. Math. 157(2004), no. 2, 227 -274.Google Scholar
[2] Cohen, A. M., van Leeuwen, M. A. A., and Lisser, B., Li E: A package for Lie group computations. Computer Algebra Nederland, Amsterdam, 1992.Google Scholar
[3] Derksen, H. and Weyman, J., Semi-invariants of quivers and saturation for Littlewood–Richardson coefficients. J. Amer. Math. Soc. 13(2000), no. 3, 467–479.Google Scholar
[4] Enright, T. J., Hunziker, M., and Wallach, N. R., A Pieri rule for Hermitian symmetric pairs I. Pacific J. Math. 214(2004), no. 1, 23–30.Google Scholar
[5] Enright, T. J. and Wallach, N. R., A Pieri rule for Hermitian symmetric pairs II. Pacific J. Math. 216(2004), no. 1, 51–61.Google Scholar
[6] Goodman, R. and Wallach, N. R., Representations and invariants of the classical groups. In: Encyclopedia of mathematics and its applications 68, Cambridge University Press, Cambridge, 1998.Google Scholar
[7] Garcia, A. M. and Remmel, J., Plethystic formulas and positivity for q, t -Kostka coefficients. In: Mathematical essays in honor of Gian-Carlo Rota, Progr. Math. 161, Birkhäuser Boston, Boston, MA, 1998, pp. 245–262.Google Scholar
[8] Garcia, A. M. and Tesler, G., Plethystic formulas for Macdonald q , t -Kostka coefficients. Adv. Math. 123(1996), no. 2, 144–222.Google Scholar
[9] Harish-Chandra, , Spherical functions on a semisimple Lie group. I. Amer. J. Math. 80(1958), 241–310.Google Scholar
[10] Helgason, S., Differential geometry, Lie groups, and symmetric spaces. Pure and Applied Mathematics 80, Academic Press, Inc., New York-London, 1978.Google Scholar
[11] Helgason, S., Groups and geometric analysis. Integral geometry, invariant differential operators, and spherical functions. Pure and Applied Mathematics 113, Academic Press, Inc., Orlando, FL, 1984.Google Scholar
[12] Howe, R., E.-C. Tan, and Willenbring, J. F., Stable branching rules for classical symmetric pairs. Trans. Amer. Math. Soc. 357(2005), no. 4, 1601–1626.Google Scholar
[13] Humphreys, J. E., Introduction to Lie algebras and representation theory. Second printing, revised. Graduate Texts in Mathematics 9. Springer-Verlag, New York-Berlin, 1978.Google Scholar
[14] Johnson, K. D., On a ring of invariant polynomials on a Hermitian symmetric space. J. Algebra 67(1980), no. 1, 72–81.Google Scholar
[15] Kac, V. G., Some remarks on nilpotent orbits. J. Algebra 64(1980), no. 1, 190–213.Google Scholar
[16] Anatol, A. N. and Noumi, M., Affine Hecke algebras and raising operators for Macdonald polynomials. Duke Math. J. 93(1998), no. 1, 1–39.Google Scholar
[17] Klyachko, A. A., Stable bundles, representation theory and Hermitian operators. Selecta Math. 4(1998), no. 3, 419–445.Google Scholar
[18] Knop, F., Integrality of two variable Kostka functions. J. Reine Angew. Math. 482(1997), 177–189.Google Scholar
[19] Knop, F., Some remarks on multiplicity free spaces. In: Representation theories and algebraic geometry, NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 514, Kluwer Acad. Publ., Dordrecht, 1998, pp. 301–317.Google Scholar
[20] Knop, F. and Sahi, S., A recursion and a combinatorial formula for Jack polynomials. Invent. Math. 128(1997), no. 1, 9–22.Google Scholar
[21] Knutson, A. and Tao, T., The honeycomb model of GLn (C) tensor products. I. Proof of the saturation conjecture. J. Amer. Math. Soc. 12(1999), no. 4, 1055–1090.Google Scholar
[22] Korányi, A. and Wolf, J. A., Realization of hermitian symmetric spaces as generalized half-planes. Ann. of Math. 81(1965), 265–288.Google Scholar
[23] Lapointe, L. and Vinet, L., A Rodrigues formula for the Jack polynomials and the Macdonald-Stanley conjecture. Internat. Math. Res. Notices 1995, no. 9, 419–424.Google Scholar
[24] Loos, O., Symmetric spaces. I: General theory. W. A. Benjamin, Inc., New York-Amsterdam, 1969.Google Scholar
[25] Moore, C. C., Compactifications of symmetric spaces. II. the Cartan domains. Amer. J. Math. 86(1964), 358–378.Google Scholar
[26] Macdonald, I. G., Symmetric functions and Hall polynomials. Second edition, Oxford Mathematical Monographs, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1995.Google Scholar
[27] Richardson, R. W., Orbits, invariants, and representations associated to involutions of reductive groups. Invent. Math. 66(1982), no. 2, 287–312.Google Scholar
[28] Ruitenburg, G. C. M., Invariant ideals of polynomial algebras with multiplicity free group action. Compositio Math. 71(1989), 181–227.Google Scholar
[29] Sahi, S., Interpolation, integrality, and a generalization of Macdonald's polynomials. Internat. Math. Res. Notices (1996), no. 10, 457–471.Google Scholar
[30] Schlichtkrull, H., One-dimensional K-types in finite-dimensional representations of semisimple Lie groups: a generalization of Helgason's theorem. Math. Scand. 54(1984), no. 2, 279–294.Google Scholar
[31] Schmid, W., Die Randwerte holomorpher Funktionen auf hermitesch symmetrischen Räumen. Invent. Math. 9(1969/1970), 61–80.Google Scholar
[32] Stanley, R. P., Some combinatorial properties of Jack symmetric functions. Adv. Math. 77(1989), no. 1, 76–115.Google Scholar
[33] Vust, T., Opération de groupes réductifs dans un type de cônes presque homogènes. Bull. Soc. Math. France 102(1974), 317-333.Google Scholar
[34] Wallach, N. R., The analytic continuation of the discrete series II. Trans. Amer. Math. Soc. 251(1979), 19–37.Google Scholar