No CrossRef data available.
Article contents
Characterizing Complete Erdős Space
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The space now known as complete Erdős space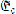
${{\mathfrak{E}}_{\text{c}}}$ was introduced by Paul Erdős in 1940 as the closed subspace of the Hilbert space 
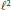${{\ell }^{2}}$ consisting of all vectors such that every coordinate is in the convergent sequence 
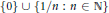$\left\{ 0 \right\}\cup \left\{ 1/n:n\in \mathbb{N}\ \right\}$. In a solution to a problem posed by Lex 
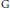$G$. Oversteegen we present simple and useful topological characterizations of 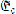${{\mathfrak{E}}_{\text{c}}}$. As an application we determine the class of factors of 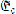${{\mathfrak{E}}_{\text{c}}}$. In another application we determine precisely which of the spaces that can be constructed in the Banach spaces 
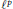${{\ell }^{p}}$ according to the ‘Erdős method’ are homeomorphic to 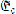${{\mathfrak{E}}_{\text{c}}}$. A novel application states that if 
$I$ is a Polishable 
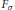${{F}_{\sigma }}$-ideal on 
$\omega $, then $I$ with the Polish topology is homeomorphic to either 
$\mathbb{Z}$, the Cantor set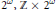 
${{2}^{\omega }},\,\mathbb{Z}\,\times \,{{2}^{\omega }}$, or 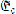${{\mathfrak{E}}_{\text{c}}}$. This last result answers a question that was asked by Stevo Todorčević.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[1]
Aarts, J. M. and Oversteegen, L. G., The geometry of Julia sets. Trans. Amer. Math. Soc. 338 (1993), no. 2, 897–918.Google Scholar
[2]
Abry, M. and Dijkstra, J. J., On topological Kadec norms. Math. Ann. 332 (2005), no. 4, 759–765.Google Scholar
[3]
Ancel, F. D., Dobrowolski, T., and Grabowski, J., Closed subgroups in Banach spaces. StudiaMath. 109 (1994), no. 3, 277–290.Google Scholar
[4]
Bessaga, C. and Pełczyński, A, Selected Topics in infinite-dimensional topology.
Monografie Matematyczne 58, PWN–Polish Scientific Publishers, Warsaw, 1975.Google Scholar
[5]
Bula, W. D. and Oversteegen, L. G., A characterization of smooth Cantor bouquets. Proc. Amer. Math. Soc. 108 (1990), no. 2, 529–534.Google Scholar
[6]
Charatonik, W. J., The Lelek fan is unique. Houston J. Math. 15 (1989), no. 1, 27–34.Google Scholar
[7]
Davis, W. J. andJohnson, W. B., A renorming of nonreflexive Banach spaces. Proc. Amer. Math. Soc. 37 (1973), 486–488.Google Scholar
[8]
Davis, W. J. and Lindenstrauss, J., On total nonnorming subspaces. Proc. Amer. Math. Soc. 31 (1972), 109–111.Google Scholar
[9]
Dijkstra, J. J., A criterion for Erdʺos spaces. Proc. Edinb. Math. Soc. (2) 48 (2005), no. 3, 595–601.Google Scholar
[10]
Dijkstra, J. J., A homogeneous space that is one-dimensional but not cohesive. Houston J. Math. 32 (2006), no. 4, 1093–1099.Google Scholar
[11]
Dijkstra, J. J., Characterizing stable complete Erdʺos space. www.few.vu.nl/~dijkstra/research/papers/stable.pdfGoogle Scholar
[12]
Dijkstra, J. J. and van Mill, J., Homeomorphism groups of manifolds and Erdʺos space. Electron. Res. Announc. Amer. Math. Soc. 10 (2004), 29–38.Google Scholar
[13]
Dijkstra, J. J. and van Mill, J., A counterexample concerning line-free groups and complete Erdʺos space. Proc. Amer. Math. Soc. 134 (2006), no. 8, 2281–2283.Google Scholar
[14]
Dijkstra, J. J. and van Mill, J.. Erdʺos space and homeomorphism groups of manifolds. Mem. Amer. Math. Soc., to appear.Google Scholar
[15]
Dijkstra, J. J., van Mill, J., and Steprans, J., Complete Erdős space is unstable, Math. Proc. Cambridge Philos. Soc. 137 (2004), 465–473.Google Scholar
[16]
Dijkstra, J. J., van Mill, J., and Valkenburg, K. I. S., On nonseparable Erdʺos spaces. J. Math. Soc. Japan 60 (2008), no. 3, 793–818.Google Scholar
[17]
Dobrowolski, T. and Grabowski, J., Subgroups of Hilbert spaces. Math. Z. 211 (1992), no. 4, 657–669.Google Scholar
[18]
Dobrowolski, T., Grabowski, J., and Kawamura, K., Topological type of weakly closed subgroups in Banach spaces. StudiaMath. 118 (1996), no. 1, 49–62.Google Scholar
[19]
van Engelen, A. J. M., Homogeneous zero-dimensional absolute Borel sets, CWI Tract, Vol. 27, Centre for Mathematics and Computer Science, Amsterdam, 1986.Google Scholar
[20]
Erdʺos, P., The dimension of the rational points in Hilbert space. Ann. of Math. 41 (1940), 734–736.Google Scholar
[21]
Farah, I., Analytic quotients: theory of liftings for quotients over analytic ideals on the integers. Mem. Amer. Math. Soc. 148 (2000), no. 702.Google Scholar
[22]
Kawamura, K., Oversteegen, L. G., and Tymchatyn, E. D., On homogeneous totally disconnected 1-dimensional spaces. Fund. Math. 150 (1996), no. 2, 97–112.Google Scholar
[23]
Kechris, A. S., Classical descriptive set theory.
Graduate Texts in Mathematics 156, Springer-Verlag, New York, 1995.Google Scholar
[24]
Kechris, A. S. and Louveau, A., The classification of hypersmooth Borel equivalence relations. J. Amer. Math. Soc. 10 (1997), no. 1, 215–242.Google Scholar
[25]
Lelek, A., On plane dendroids and their end points in the classical sense. Fund. Math. 49 (1960/1961), 301–319.Google Scholar
[26]
Mayer, J. C., An explosion point for the set of endpoints of the Julia set of ƛ exp(z). Ergodic Theory Dynam. Systems 10 (1990), no. 1, 177–183.Google Scholar
[27]
Mayer, J. C., Nikiel, J., and Oversteegen, L. G., Universal spaces for R-trees. Trans. Amer.Math. Soc. 334 (1992), no. 1, 411–432.Google Scholar
[28]
Mayer, J. C. and Oversteegen, L. G., A topological characterization of R-trees. Trans. Amer.Math. Soc. 320 (1990), no. 1, 395–415.Google Scholar
[29]
Mayer, J. C. and Oversteegen, L. G., Continuum theory. In: Recent Progress in General Topology, North-Holland, Amsterdam, 1992, pp. 453–492.Google Scholar
[30]
Oversteegen, L. G. and Tymchatyn, E. D., On the dimension of certain totally disconnected spaces. Proc. Amer. Math. Soc. 122 (1994), no. 3, 885–891.Google Scholar
[32]
Solecki, S., Analytic ideals and their applications. Ann. Pure Appl. Logic 99 (1999), no. 1-3, 51–72.Google Scholar
[34]
Trnková, V., Xm is homeomorphic to Xniffm n where is a congruence on natural numbers. Fund. Math. 80 (1973), no. 1, 51–56.Google Scholar
You have
Access