Hostname: page-component-5cf477f64f-tx7qf Total loading time: 0 Render date: 2025-04-02T08:30:54.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Face Ring Multiplicity via CM-Connectivity Sequences

Published online by Cambridge University Press:  20 November 2018

Isabella Novik  and
Ed Swartz
Isabella Novik
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195-4350, USA, e-mail:[email protected]
Ed Swartz
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195-4350, USA, e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The multiplicity conjecture of Herzog, Huneke, and Srinivasan is verified for the face rings of the following classes of simplicial complexes: matroid complexes, complexes of dimension one and two, and Gorenstein complexes of dimension at most four. The lower bound part of this conjecture is also established for the face rings of all doubly Cohen–Macaulay complexes whose 1-skeleton's connectivity does not exceed the codimension plus one as well as for all 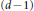$\text{(}d-1)$-dimensional $d$-Cohen–Macaulay complexes. The main ingredient of the proofs is a new interpretation of the minimal shifts in the resolution of the face ring 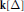$\mathbf{k}[\Delta ]$ via the Cohen–Macaulay connectivity of the skeletons of $\Delta $.

Keywords

13F5552B0513H1513D0205B35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 4 , 01 August 2009 , pp. 888 - 903
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Baclawski, K., Cohen–Macaulay connectivity and geometric lattices. European J. Combin. 3(1982), 293–305.Google Scholar
[2] Bruns, W. and Herzog, J., Cohen–Macaulay Rings. Cambridge Studies in Advanced Mathematics 39. Cambridge University Press, Cambridge, 1993.Google Scholar
[3] Bruns, W. and Hibi, T., Stanley-Reisner rings with pure resolutions. Comm. Algebra 23(1995), 1201–1217.Google Scholar
[4] Bruns, W. and Hibi, T., Cohen–Macaulay partially ordered sets with pure resolutions. European J. Combin. 19(1998), no. 7, 779–785.Google Scholar
[5] Fløystad, G., Cohen–Macaulay cell complexes,. In: Algebraic and Geometric Combinatorics. Contemp. Math. 423, American Mathematical Society, Providence, RI, 2006, pp. 205–220.Google Scholar
[6] Francisco, C. A., New approaches to bounding the multiplicity of an ideal. J. Algebra 299(2006), no. 1, 309–328.Google Scholar
[7] Francisco, C. A. and Srinivasan, H., Multiplicity conjectures. In: Syzygies and Hilbert Functions. Lect. Notes Pure Appl. Math. 254. Chapman & Hall, Boca Raton, Fl, 2007, pp. 145–178.Google Scholar
[8] Garnick, K., Kwong, Y. H. H., and Lazebnik, F., Extremal graphs without three cycles or four cycles. J. Graph Theory 17(1993), no. 5, 633–645.Google Scholar
[9] Gold, L. H., A degree bound for codimension two lattice ideals. J. Pure Appl. Algebra 182(2003), no. 2-3, 201–207.Google Scholar
[10] Gold, L., Schenck, H., and Srinivasan, H., Betti numbers and degree bounds for some linked zero schemes. J. Pure Appl. Algebra 210(2007), no. 2, 481–491.Google Scholar
[11] Guardo, E. and Van Tuyl, A., Powers of complete intersections: graded Betti numbers and applications. Illinois J. Math. 49(2005), no. 1, 265–279.Google Scholar
[12] Herzog, J. and Srinivasan, H., Bounds for multiplicities. Trans. Amer. Math. Soc. 350(1998), no. 7, 2879–2902.Google Scholar
[13] Herzog, J. and Zheng, X., Notes on the multiplicity conjecture. Collect. Math. 57(2006), no. 2, 211–226.Google Scholar
[14] Hibi, T., Level rings and algebras with straightening laws. J. Algebra 117(1988), no. 2, 343–362.Google Scholar
[15] Hochster, M., Cohen-Macaulay rings, combinatorics, and simplicial complexes. In: Ring Theory. II. Lect. Notes Pure Appl. Math 26. Dekker, NY, 1977, pp. 171–223.Google Scholar
[16] Huneke, C. and Miller, M., A note on the multiplicity of Cohen-Macaulay algebras with pure resolutions. Canad. J. Math. 37(1985), no. 6, 1149–1162.Google Scholar
[17] Klee, V., A combinatorial analogue of Poincaré's duality theorem. Canad. J. Math. 16(1964), 517–531.Google Scholar
[18] Kubitzke, M. and Welker, V., The multiplicity conjecture for barycentric subdivisions. Comm. Algebra 36(2008), no. 11, 4223–4248.Google Scholar
[19] Migliore, J., Nagel, U., and Römer, T., The multiplicity conjecture in low codimensions.Math. Res. Lett. 12(2005), no. 5-6, 731–747.Google Scholar
[20] Migliore, J., Nagel, U., and Römer, T., Extensions of the multiplicity conjecture. Trans. Amer. Math. Soc. 360(2008), no. 6, 2965–2985.Google Scholar
[21] Miró-Roig, R., A note on the multiplicity of determinantal ideals. J. Algebra 299(2006), no. 2, 714–724.Google Scholar
[22] Nicoletti, G. and White, N., Axiom systems. In: Theory of Matroids. Encyclopedia Math. Appl. 26, Cambridge University Press, Cambridge, 1986, pp. 29–44.Google Scholar
[23] Novik, I., Postnikov, A., and Sturmfels, B., Syzygies of oriented matroids. Duke Math. J. 111(2002), no. 2, 287–317.Google Scholar
[24] Reisner, G., Cohen-Macaulay quotients of polynomial rings. Adv. in Math. 21(1976), no. 1, 30–49.Google Scholar
[25] Römer, T., Note on bounds for multiplicities. J. Pure Appl. Algebra 195(2005), no. 1, 113–123.Google Scholar
[26] Srinivasan, H., A note on the multiplicities of Gorenstein algebras. J. Algebra 208(1998), no. 2, 425–443.Google Scholar
[27] Stanley, R., The upper bound conjecture and Cohen-Macaulay rings. Stud. Appl. Math. 54(1975), no. 2, 135–142.Google Scholar
[28] Stanley, R., Combinatorics and Commutative Algebra. Second Edition, Birkhäuser Boston, Boston, MA, 1996.Google Scholar
[29] van Lint, J. H. and Wilson, R. M., A Course in Combinatorics. Cambridge University Press, Cambridge, 1992.Google Scholar