Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-18T12:58:19.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Čebyšev Sets in Hyperspaces over Rn

Published online by Cambridge University Press:  20 November 2018

Robert J. MacG. Dawson  and
Maria Moszyńska
Robert J. MacG. Dawson
Affiliation:
Dept. of Mathematics and, Computing Science, Saint Mary’s University, Halifax, Nova Scotia, Canada, [email protected]
Maria Moszyńska
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A set in a metric space is called a Čebyšev set if it has a unique “nearest neighbour” to each point of the space. In this paper we generalize this notion, defining a set to be Čebyšev relative to another set if every point in the second set has a unique “nearest neighbour” in the first. We are interested in Čebyšev sets in some hyperspaces over 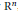${{\text{R}}^{n}}$, endowed with the Hausdorff metric, mainly the hyperspaces of compact sets, compact convex sets, and strictly convex compact sets.

We present some new classes of Čebyšev and relatively Čebyšev sets in various hyperspaces. In particular, we show that certain nested families of sets are Čebyšev. As these families are characterized purely in terms of containment,without reference to the semi-linear structure of the underlyingmetric space, their properties differ markedly from those of known Čebyšev sets.

Keywords

41A5252A20convex bodystrictly convex setČebyšv setrelative Čebyšv setnested familystrongly nested familyfamily of translates
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 299 - 314
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bazilevich, L. E., Topology of the hyperspace of convex bodies of constant width. Math. Notes 62(1997), no. 5-6, 683–687.Google Scholar
[2] Blumenthal, L. M., Theory and applications of distance geometry. Oxford University Press, 1953.Google Scholar
[3] Bogdewicz, A. and Moszyńska, M., Čebyšev sets in the space of convex bodies. Rend. Circ. Mat. Palermo, Suppl. 77(2006), 19–39.Google Scholar
[4] Braess, D., Nonlinear approximation theory. Springer Series in Computational Mathematics 7, Springer-Verlag, Berlin, 1986.Google Scholar
[5] Federer, H., Curvature measures. Trans. Amer. Math. 93(1959), 418–481.Google Scholar
[6] Jongmans, F., De l'art d’être à bonne distance des ensembles dont la décomposition atteint un stade avancé. Bull. Soc. Roy. Sci. Li ège 48(1979), no. 9-10, 237–261.Google Scholar
[7] Klee, V., Convexity of Čebyšev sets. Math. Ann. 142(1960/1961), 292–304.Google Scholar
[8] Moszyńska, M., Selected topics in convex geometry. Birkhäuser, Boston, MA, 2006.Google Scholar
[9] Schneider, R., Convex bodies: the Brunn–Minkowski theory. Encyclopedia of Mathematics and its Applications 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[10] Singer, I., Best approximation in normed linear spaces by elements of linear subspaces. Springer-Verlag, New York-Berlin, 1970.Google Scholar
[11] Vitale, R. A., Lp metrics for compact, convex sets. J. Approx. Theory 45(1985), no. 3, 280–287.Google Scholar