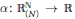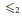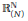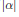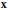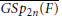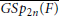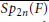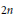Research Article
On the Local Convexity of Intersection Bodies of Revolution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-27
-
- Article
-
- You have access
- Export citation
Bounded Derived Categories of Infinite Quivers: Grothendieck Duality, Reflection Functor
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-54
-
- Article
-
- You have access
- Export citation
On Varieties of Lie Algebras of Maximal Class
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-89
-
- Article
-
- You have access
- Export citation
Une propriété de domination convexe pour les orbites sturmiennes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 90-106
-
- Article
-
- You have access
- Export citation
The Weyl Problem With Nonnegative Gauss Curvature In Hyperbolic Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-131
-
- Article
-
- You have access
- Export citation
Unitary Equivalence and Similarity to Jordan Models for Weak Contractions of Class C0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 132-151
-
- Article
-
- You have access
- Export citation
On Homotopy Invariants of Combings of Three-manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 152-183
-
- Article
-
- You have access
- Export citation
Geometric Spectra and Commensurability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-197
-
- Article
-
- You have access
- Export citation
Tate Cycles on Abelian Varieties with Complex Multiplication
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-213
-
- Article
-
- You have access
- Export citation
Symmetric Genuine Spherical Whittaker Functions on
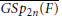
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 214-240
-
- Article
-
- You have access
- Export citation