Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T17:48:02.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Unitary Equivalence and Similarity to Jordan Models for Weak Contractions of Class C0

Published online by Cambridge University Press:  20 November 2018

Raphaël Clouâtre
Raphaël Clouâtre*
Affiliation:
Department of Pure Mathematics, University of Waterloo, 200 University Ave. West, Waterloo ON, N2L 3G1. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain results on the unitary equivalence of weak contractions of class 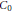${{C}_{0}}$ to their Jordan models under an assumption on their commutants. In particular, our work addresses the case of arbitrary finite multiplicity. The main tool in this paper is the theory of boundary representations due to Arveson. We also generalize and improve previously known results concerning unitary equivalence and similarity to Jordan models when the minimal function is a Blaschke product.

Keywords

47A4547L55weak contractionsoperators of class C0Jordan modelunitary equivalence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 132 - 151
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Apostol, C., Inner derivations with closed range. Rev. Roumaine Math. Pures Appl. 21(1976), no. 3, 249–265.Google Scholar
[2] Arveson, W. B., Subalgebras of C*-algebras. Acta Math. 123(1969), 141–224.http://dx.doi.org/10.1007/BF02392388 Google Scholar
[3] Arveson, W. B., Subalgebras of C*-algebras. II. Acta Math. 128(1972), no. 3–4, 271–308. http://dx.doi.org/10.1007/BF02392166 Google Scholar
[4] Bercovici, H., Operator theory and arithmetic in H∞ . Mathematical Surveys and Monographs, 26, American Mathematical Society, Providence, RI, 1988.Google Scholar
[5] Bercovici, H., Foiaş, C., and Sz.-Nagy, B., Compléments à l’étude des opérateurs de classe C0. III. Acta Sci. Math. (Szeged) 37(1975), no. 3–4, 313–322.Google Scholar
[6] Bercovici, H. and Voiculescu, D., Tensor operations on characteristic functions of C0contractions. Acta Sci. Math. (Szeged) 39(1977), no. 3–4, 205–231.Google Scholar
[7] Carleson, L., Interpolations by bounded analytic functions and the corona problem. Ann. of Math. (2) 76(1962), 547–559. http://dx.doi.org/10.2307/1970375 Google Scholar
[8] Clouâtre, R., Similarity results for operators of class C0. Integral Equations Operator Theory, 71(2011), no. 4, 557–573.http://dx.doi.org/10.1007/s00020-011-1916-x Google Scholar
[9] Clouâtre, R., Similarity results for operators of class C0and the algebra H∞1(T)..Oper. Matrices, to appear. http://dx.doi.org/10.1007/s00020-011-1916-x Google Scholar
[10] Davidson, K. R., C*-algebras by example. Fields Institute Monographs, 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
[11] Herrero, D. A., The exceptional subset of a C0-contraction. Trans. Amer. Math. Soc. 173(1972), 93–115.Google Scholar
[12] Jiang, C. and Yang, R., Jordan blocks and strong irreducibility. New York J. Math. 17(2011), 619–626.Google Scholar
[13] Moore, B., III and Nordgren, E., On transitive algebras containing C0operators. Indiana Univ. Math. J. 24(1974/75), 777–784.http://dx.doi.org/10.1512/iumj.1975.24.24062 Google Scholar
[14] Nikolski, N. K., Operators, functions, and systems: an easy reading. Vol. 2. Model operators and systems. Mathematical Surveys and Monographs, 93, American Mathematical Society, Providence, RI, 2002.Google Scholar
[15] Nikolski, S. M., Spectral theory of functions and operators. A translation of Trudy Mat. Inst. Steklov. 130(1978), Proc. Steklov Inst. Math. (1979), no. 4, American Mathematical Society, Providence, RI, 1979.Google Scholar
[16] Paulsen, V., Completely bounded maps and operator algebras. Cambridge Studies in Advanced Mathematics, 78, Cambridge University Press, Cambridge, 2002.Google Scholar
[17] Sarason, D., Generalized interpolation in H∞1. Trans. Amer. Math. Soc. 127(1967), 179–203. Google Scholar
[18] -Nagy, B. Sz. and Foiaş, C., Compléments à l’étude des opérateurs de classe C0. Acta Sci. Math. (Szeged), 31(1970), 287–296.Google Scholar
[19] -Nagy, B. Sz. and Foiaş, C., Local characterization of operators of class C0. J. Functional Analysis 8(1971), 76–81. http://dx.doi.org/10.1016/0022-1236(71)90019-X Google Scholar
[20] -Nagy, B.Sz., Foias, C., Bercovici, H., and Kérchy, L., Harmonic analysis of operators on Hilbert space. Second ed., Universitext, Springer, New York, 2010.Google Scholar
[21] Vasyunin, V. I., Unconditionally convergent spectral expansions, and nonclassical interpolation. (Russian) Dokl. Akad. Nauk SSSR 227(1976), no. 1, 11–14.Google Scholar
[22] Williams, L. R., Similarity invariants for a class of nilpotent operators. Acta Sci. Math. (Szeged)38(1976), no. 3–4, 423–428.Google Scholar