Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fillastre, François
Izmestiev, Ivan
and
Veronelli, Giona
2016.
Hyperbolization of cusps with convex boundary.
Manuscripta Mathematica,
Vol. 150,
Issue. 3-4,
p.
475.
Guan, Pengfei
and
Lu, Siyuan
2017.
Curvature estimates for immersed hypersurfaces in Riemannian manifolds.
Inventiones mathematicae,
Vol. 208,
Issue. 1,
p.
191.
Li, Chunhe
Miao, Pengzi
and
Wang, Zhizhang
2019.
Uniqueness of isometric immersions with the same mean curvature.
Journal of Functional Analysis,
Vol. 276,
Issue. 9,
p.
2831.
Lu, Siyuan
2020.
On Weyl’s Embedding Problem in Riemannian Manifolds.
International Mathematics Research Notices,
Vol. 2020,
Issue. 11,
p.
3229.
Chen, Po-Ning
and
Zhang, Xiangwen
2020.
A Rigidity Theorem for Surfaces in Schwarzschild Manifold.
International Mathematics Research Notices,
Vol. 2020,
Issue. 16,
p.
4833.
Li, Siran
2021.
The Weyl problem of isometric immersions revisited.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 1,
p.
220.
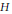 $H$ and extend the result to
$H$ and extend the result to 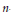 $n$-dimensions. We also obtain an estimate for the gradient of the smaller principal curvature in 2 dimensions.
$n$-dimensions. We also obtain an estimate for the gradient of the smaller principal curvature in 2 dimensions.