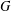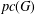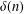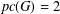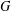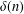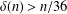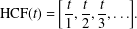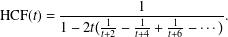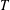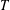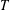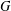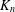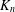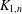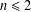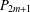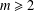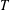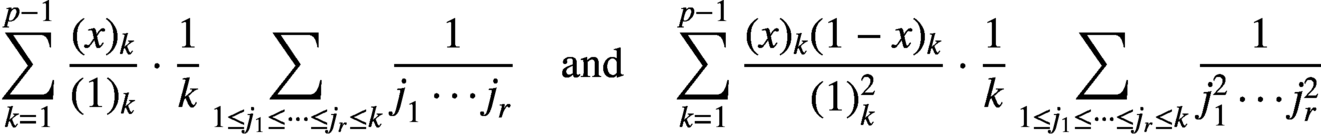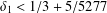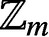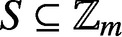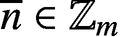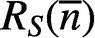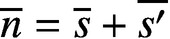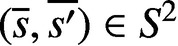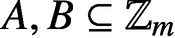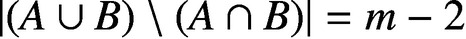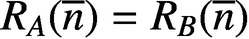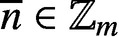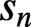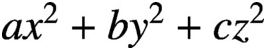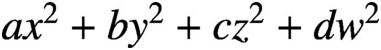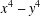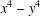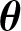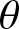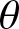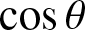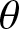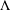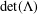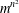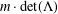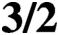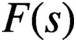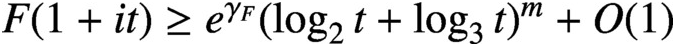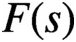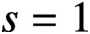Research Article
NOTE ON MINIMUM DEGREE AND PROPER CONNECTION NUMBER
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2020, pp. 177-181
-
- Article
- Export citation
SUMS OF PARTIAL THETA FUNCTIONS THROUGH AN EXTENDED BAILEY TRANSFORM
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2020, pp. 1-10
-
- Article
- Export citation
MULTINOMIAL VANDERMONDE CONVOLUTION VIA PERMANENT
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2020, pp. 353-361
-
- Article
- Export citation
THE METRIC DIMENSION OF THE ANNIHILATING-IDEAL GRAPH OF A FINITE COMMUTATIVE RING
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2021, pp. 362-368
-
- Article
- Export citation
CONNECTIVITY PROPERTIES OF MCKAY QUIVERS
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2020, pp. 182-194
-
- Article
- Export citation
AN EXACT FORMULA FOR THE HARMONIC CONTINUED FRACTION
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2020, pp. 11-21
-
- Article
- Export citation
GRAPHS DETERMINED BY THEIR
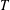 $T$-GAIN SPECTRA
$T$-GAIN SPECTRA
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2020, pp. 195-203
-
- Article
- Export citation
ON THE ARITHMETIC STRUCTURE OF RATIONAL NUMBERS IN THE CANTOR SET
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2020, pp. 22-27
-
- Article
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
-
- Article
- Export citation
TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2021, pp. 379-389
-
- Article
- Export citation
SUM-PRODUCT ESTIMATES FOR DIAGONAL MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 24 June 2020, pp. 28-37
-
- Article
- Export citation
PARTITIONS OF
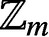 $\mathbb {Z}_m$
WITH IDENTICAL REPRESENTATION FUNCTION
$\mathbb {Z}_m$
WITH IDENTICAL REPRESENTATION FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 22 September 2020, pp. 204-209
-
- Article
- Export citation
LOOK, KNAVE
- Part of:
-
- Published online by Cambridge University Press:
- 21 October 2020, pp. 210-217
-
- Article
- Export citation
PRIME-UNIVERSAL DIAGONAL QUADRATIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 390-404
-
- Article
- Export citation
INTEGERS REPRESENTED BY
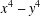 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2020, pp. 38-49
-
- Article
- Export citation
ON
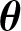 $\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
$\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2020, pp. 218-229
-
- Article
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
-
- Article
- Export citation
CONGRUENCES MODULO 4 FOR WEIGHT
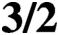 $\textbf{3/2}$
ETA-PRODUCTS
$\textbf{3/2}$
ETA-PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 405-417
-
- Article
- Export citation
ON THE POSITION OF NODES OF PLANE CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2020, pp. 62-68
-
- Article
- Export citation
LARGE VALUES OF L-FUNCTIONS ON THE 1-LINE
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2020, pp. 230-243
-
- Article
- Export citation