No CrossRef data available.
Article contents
ON THE POSITION OF NODES OF PLANE CURVES
Published online by Cambridge University Press: 01 June 2020
Abstract
The Severi variety 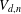 $V_{d,n}$ of plane curves of a given degree
$V_{d,n}$ of plane curves of a given degree 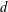 $d$ and exactly
$d$ and exactly  $n$ nodes admits a map to the Hilbert scheme
$n$ nodes admits a map to the Hilbert scheme 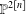 $\mathbb{P}^{2[n]}$ of zero-dimensional subschemes of
$\mathbb{P}^{2[n]}$ of zero-dimensional subschemes of 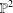 $\mathbb{P}^{2}$ of degree
$\mathbb{P}^{2}$ of degree  $n$. This map assigns to every curve
$n$. This map assigns to every curve 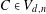 $C\in V_{d,n}$ its nodes. For some
$C\in V_{d,n}$ its nodes. For some  $n$, we consider the image under this map of many known divisors of the Severi variety and its partial compactification. We compute the divisor classes of such images in
$n$, we consider the image under this map of many known divisors of the Severi variety and its partial compactification. We compute the divisor classes of such images in 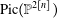 $\text{Pic}(\mathbb{P}^{2[n]})$ and provide enumerative numbers of nodal curves. We also answer directly a question of Diaz–Harris [‘Geometry of the Severi variety’, Trans. Amer. Math. Soc.309 (1988), 1–34] about whether the canonical class of the Severi variety is effective.
$\text{Pic}(\mathbb{P}^{2[n]})$ and provide enumerative numbers of nodal curves. We also answer directly a question of Diaz–Harris [‘Geometry of the Severi variety’, Trans. Amer. Math. Soc.309 (1988), 1–34] about whether the canonical class of the Severi variety is effective.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 62 - 68
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
During the preparation of this article the first named author was partly supported by the CONACYT grant CB-2015/253061; he is currently a CONACYT Research Fellow in Mathematics, project no. 1036.



