Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T10:49:22.175Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTE ON MINIMUM DEGREE AND PROPER CONNECTION NUMBER

Part of: Graph theory

Published online by Cambridge University Press:  03 July 2020

YUEYU WU Open the ORCID record for YUEYU WU [Opens in a new window] ,
YUNQING ZHANG Open the ORCID record for YUNQING ZHANG [Opens in a new window]  and
YAOJUN CHEN Open the ORCID record for YAOJUN CHEN [Opens in a new window]
YUEYU WU
Affiliation:
Department of Mathematics, Nanjing University, Nanjing210093, PR China email [email protected]
YUNQING ZHANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing210093, PR China email [email protected]
YAOJUN CHEN*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing210093, PR China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An edge-coloured graph 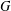$G$ is called properly connected if any two vertices are connected by a properly coloured path. The proper connection number, 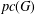$pc(G)$, of a graph 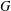$G$, is the smallest number of colours that are needed to colour 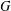$G$ such that it is properly connected. Let 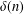$\unicode[STIX]{x1D6FF}(n)$ denote the minimum value such that 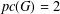$pc(G)=2$ for any 2-connected incomplete graph 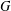$G$ of order $n$ with minimum degree at least 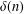$\unicode[STIX]{x1D6FF}(n)$. Brause et al. [‘Minimum degree conditions for the proper connection number of graphs’, Graphs Combin.33 (2017), 833–843] showed that 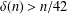$\unicode[STIX]{x1D6FF}(n)>n/42$. In this note, we show that 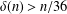$\unicode[STIX]{x1D6FF}(n)>n/36$.

Keywords

proper colouringproper connection numberminimum degree

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C07: Vertex degrees 05C40: Connectivity
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 177 - 181
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by NSFC under Grant Nos 11671198, 11871270 and 11931006.

References

Borozan, V., Fujita, S., Gerek, A., Magnant, C., Manoussakis, Y., Montero, L. and Tuza, Z., ‘Proper connection of graphs’, Discrete Math. 312 (2012), 2550–2560.Google Scholar
Brause, C., Doan, T. and Schiermeyer, I., ‘Minimum degree conditions for the proper connection number of graphs’, Graphs Combin. 33 (2017), 833–843.Google Scholar
Huang, F., Li, X., Qin, Z., Magnant, C. and Ozeki, K., ‘On two conjectures about the proper connection number of graphs’, Discrete Math. 340 (2017), 2217–2222.Google Scholar
Vizing, V., ‘On an estimate of the chromatic class of a p-graph’, Diskret. Analiz 3 (1964), 25–30.Google Scholar