Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T04:19:49.023Z Has data issue: false hasContentIssue false
  • English
  • Français

LARGE VALUES OF L-FUNCTIONS ON THE 1-LINE

Part of: Algebraic number theory: global fields Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  02 October 2020

ANUP B. DIXIT Open the ORCID record for ANUP B. DIXIT [Opens in a new window]  and
KAMALAKSHYA MAHATAB Open the ORCID record for KAMALAKSHYA MAHATAB [Opens in a new window]
ANUP B. DIXIT*
Affiliation:
Department of Mathematics and Statistics, Queen’s University, Jeffery Hall, 48 University Ave Kingston, Ontario K7L 3N8, Canada
KAMALAKSHYA MAHATAB
Affiliation:
Department of Mathematics and Statistics, University of Helsink, P. O. Box 68, FIN 00014 Helsinki, Finland e-mail: [email protected], [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study lower bounds of a general family of L-functions on the 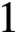$1$ -line. More precisely, we show that for any 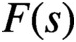$F(s)$ in this family, there exist arbitrarily large t such that 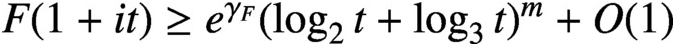$F(1+it)\geq e^{\gamma _F} (\log _2 t + \log _3 t)^m + O(1)$ , where m is the order of the pole of 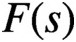$F(s)$ at 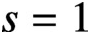$s=1$ . 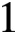This is a generalisation of the result of Aistleitner, Munsch and Mahatab [‘Extreme values of the Riemann zeta function on the $1$ -line’, Int. Math. Res. Not. IMRN2019(22) (2019), 6924–6932]. As a consequence, we get lower bounds for large values of Dedekind zeta-functions and Rankin-Selberg L-functions of the type 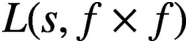$L(s,f\times f)$ on the 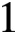$1$ -line.

Keywords

Dedekind zeta functionvalues on the 1-line

MSC classification

Primary: 11M41: Other Dirichlet series and zeta functions
Secondary: 11R42: Zeta functions and $L$-functions of number fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 230 - 243
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the Coleman postdoctoral fellowship of Queen’s University. The second author is supported by Grant 227768 of the Research Council of Norway and Project 1309940 of the Finnish Academy.

References

Aistleitner, C., ‘Lower bounds for the maximum of the Riemann zeta function along vertical lines’, Math. Ann. 365(1–2) (2016), 473–496.CrossRefGoogle Scholar
Aistleitner, C., Mahatab, K. and Munsch, M., ‘Extreme values of the Riemann zeta function on the $1$ -line’, Int. Math. Res. Not. IMRN 2019(22) (2019), 6924–6932.CrossRefGoogle Scholar
Aistleitner, C., Mahatab, K., Munsch, M. and Peyrot, A., ‘On large values of $L\left(\sigma, \chi \right)$ ’, Q. J. Math. 70(3) (2019), 831–848.CrossRefGoogle Scholar
Aistleitner, C. and Pańkowski, Ł., ‘Large values of L-functions from the Selberg class’, J. Math. Anal. Appl. 446(1) (2017), 345–364.CrossRefGoogle Scholar
Arguin, L., Belius, D., Bourgade, P., Radziwiłł, M. and Soundararajan, K., ‘Maximum of the Riemann zeta function on a short interval of the critical line’, Comm. Pure Appl. Math. 72(3) (2019), 500–535.CrossRefGoogle Scholar
Arguin, L.-P., Ouimet, F. and Radziwiłł, M., ‘Moments of the Riemann zeta function on short intervals of the critical line’, Preprint, arXiv:1901.04061.Google Scholar
Balasubramanian, R. and Ramachandra, K., ‘On the frequency of Titchmarsh’s phenomenon for $\zeta (s)$ . III’, Proc. Indian Acad. Sci. 86 (1977), 341–351.CrossRefGoogle Scholar
Beurling, A., ‘Analyse de la loi asymptotique de la distribution des nombres premiers généralisés. I’, Acta Math. 68(1) (1937), 255–291.CrossRefGoogle Scholar
Bondarenko, A. and Seip, K., ‘Large greatest common divisor sums and extreme values of the Riemann zeta function’, Duke Math. J. 166 (2017), 1685–1701.CrossRefGoogle Scholar
de la Bretèche, R. and Tenenbaum, G., ‘Sommes de Gál et applications’, Proc. Lond. Math. Soc. (3) 119(1) (2019), 104–134.CrossRefGoogle Scholar
Dixit, A. B. and Murty, V. K., ‘The Lindelöf class of $L$ -functions, II’, Int. J. Number Theory 15(10) (2019), 2201–2221.CrossRefGoogle Scholar
Granville, A. and Soundarajan, K., ‘Extreme vaues of |ζ(1+it)|’, The Riemann Zeta Function and Related Themes: Papers in Honour of Professor K. Ramachandra, Ramanujan Mathematical Society Lecture Notes Series, 2 (International Press, Boston, MA, 2010), 65–80.Google Scholar
Kaczorowski, J. and Perelli, A., ‘On the prime number theorem for the Selberg class’, Arch. Math. 80 (2003), 255–263.Google Scholar
Levinson, N., ‘ $\varOmega$ -theorems for the Riemann zeta-function’, Acta Arith. 20 (1972), 317–330.CrossRefGoogle Scholar
Mertens, F., ‘Ein Beitrag zur analytischen Zahlentheorie’, J. reine angew. Math. 78 (1874), 46–62.Google Scholar
Montgomery, H. and Vaughan, R. C., Multiplicative Number Theory. I. Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Murty, V. K., ‘The Lindelöf class of L-functions’, in: The Conference on L-Functions (eds. Weng, L. and Kaneko, M.) (World Scientific, Singapore, 2007), 165–174.Google Scholar
Rosen, M., ‘A generalization of Mertens’ theorem’, J. Ramanujan Math. Soc. 14 (1999), 1–19.Google Scholar
du Sautoy, M., ‘Natural boundaries for Euler products of Igusa zeta functions of elliptic curves’, Int. J. Number Theory 14(8) (2018), 2317–2331.CrossRefGoogle Scholar
Selberg, A., ‘Old and new conjectures and results about a class of Dirichlet series’, Collected Papers, Vol. 2 (Springer, Berlin–Heidelberg–New York, 1991), 47–63.Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, Translated from the second French edition (1995) by Thomas, C. B., Cambridge Studies in Advanced Mathematics, 46 (Cambridge University Press, Cambridge, 1995).Google Scholar
Titchmarsh, E. C., The Theory of the Riemann-Zeta Function. 2nd edn, revised by Heath-Brown, D. R. (Clarendon Press, Oxford, 1986).Google Scholar
Yashiro, Y., ‘Mertens’ theorem and prime number theorem for Selberg class’, Preprint, 2013, arXiv:1311.0754v4.Google Scholar