Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T01:45:52.628Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGERS REPRESENTED BY 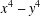$x^{4}-y^{4}$ REVISITED

Part of: Diophantine equations Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  20 May 2020

MICHAEL A. BENNETT Open the ORCID record for MICHAEL A. BENNETT [Opens in a new window]
MICHAEL A. BENNETT*
Affiliation:
Department of Mathematics,University of British Columbia, Vancouver, BC, Canada V6T 1Z2 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We sharpen earlier work of Dabrowski on near-perfect power values of the quartic form 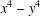$x^{4}-y^{4}$, through appeal to Frey curves of various signatures and related techniques.

Keywords

Diophantine equationsFrey curvesmodularity

MSC classification

Primary: 11D41: Higher degree equations; Fermat's equation
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F80: Galois representations 11G05: Elliptic curves over global fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 38 - 49
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by a grant from NSERC.

References

Bajolet, A., Dupuy, B., Luca, F. and Togbé, A., ‘On the Diophantine equation x 4 - q 4 = py r’, Publ. Math. Debrecen 79 (2011), 269–282.CrossRefGoogle Scholar
Bennett, M. A. and Skinner, C., ‘Ternary Diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56(1) (2004), 23–54.CrossRefGoogle Scholar
Cao, Z., ‘The Diophantine equations x 4 - y 4 = z p and x 4 - 1 = dy q’, C. R. Math. Rep. Acad. Sci. Canada 21 (1999), 23–27.Google Scholar
Capelli, A., ‘Sulla riduttibilità della funzione x n - A in un campo qualunque di razionalità’, Math. Ann. 54 (1901), 602–603.Google Scholar
Dabrowski, A., ‘On the integers represented by x 4 - y 4’, Bull. Aust. Math. Soc. 76 (2007), 133–136.CrossRefGoogle Scholar
Darmon, H., ‘The equation x 4 - y 4 = z p’, C. R. Math. Rep. Acad. Sci. Canada. 15(6) (1993), 286–290.Google Scholar
Darmon, H. and Granville, A., ‘On the equations z m = F (x, y) and Ax p + By q = Cz r’, Bull. Lond. Math. Soc. 27 (1995), 513–543.CrossRefGoogle Scholar
Darmon, H. and Merel, L., ‘Winding quotients and some variants of Fermat’s Last Theorem’, J. reine angew. Math. 490 (1997), 81–100.Google Scholar
Ivorra, W., ‘Courbes elliptiques sur ℚ, ayant un point d’ordre 2 rationnel sur ℚ, de conducteur 2Np’ (in French) [Elliptic curves over ℚ with a rational point of order 2 over ℚ and conductor 2Np]’, Dissertationes Math. (Rozprawy Mat.) 429 (2004).Google Scholar
Kraus, A., ‘Majorations effectives pour l’équation de Fermat généralisée’, Canad. J. Math. 49(6) (1997), 1139–1161.CrossRefGoogle Scholar
Kraus, A. and Oesterlé, J., ‘Sur une question de B. Mazur’, Math. Ann. 293 (1992), 259–275.Google Scholar
Luca, F. and Togbé, A., ‘On the Diophantine equation x 4 - q 4 = py 3’, Rocky Mountain J. Math. 40 (2010), 995–1008.CrossRefGoogle Scholar
Martin, G., ‘Dimensions of the spaces of cuspforms and newforms on 𝛤0(N) and 𝛤1(N)’, J. Number Theory 112 (2005), 298–331.CrossRefGoogle Scholar
Mulholland, J., ‘Elliptic Curves with Rational 2-torsion and Related Ternary Diophantine Equations’, PhD Thesis, The University of British Columbia (Canada), 2006.Google Scholar
Nagell, T., ‘L’analyse indéterminée de degré supérieur’, in: Mémorial des sciences mathématiques, Vol. 39 (Gauthier-Villars, Paris, 1929).Google Scholar
Ribet, K., ‘On modular representations of Gal(ℚ/ℚ) arising from modular forms’, Invent. Math. 100 (1990), 431–476.CrossRefGoogle Scholar
Ribet, K., ‘On the equation a p + 2𝛼b p + c p = 0’, Acta Arith. 79(1) (1997), 7–16.CrossRefGoogle Scholar
Savin, D., ‘On the Diophantine equation x 4 - q 4 = py 5’, Ital. J. Pure Appl. Math. 26 (2009), 103–108.Google Scholar
Stephens, N. M., ‘Congruence properties of congruent numbers’, Bull. Lond. Math. Soc. 7 (1975), 182–184.CrossRefGoogle Scholar
Taylor, R. L. and Wiles, A., ‘Ring theoretic properties of certain Hecke algebras’, Ann. Math. 141 (1995), 553–572.10.2307/2118560CrossRefGoogle Scholar
Wiles, A., ‘Modular elliptic curves and Fermat’s Last Theorem’, Ann. of Math. (2) 141(3) (1995), 443–551.CrossRefGoogle Scholar
Yanyan, L., ‘On the diophantine equation x 4 - q 4 = py n’, Expo. Math. 30 (2013), 196–203.CrossRefGoogle Scholar