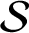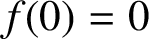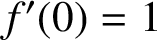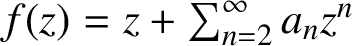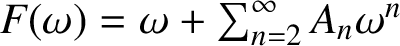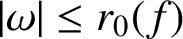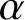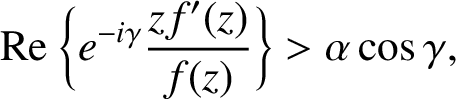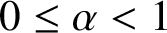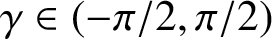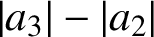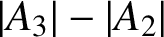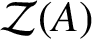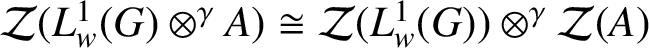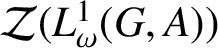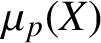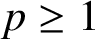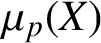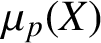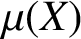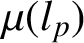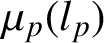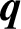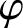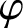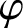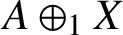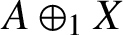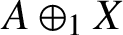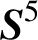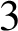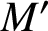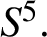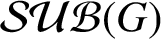Research Article
A NOTE ON SPIRALLIKE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2021, pp. 117-123
-
- Article
- Export citation
ON THE BOUNDARY BEHAVIOUR OF FRIDMAN INVARIANTS
- Part of:
-
- Published online by Cambridge University Press:
- 22 September 2021, pp. 482-489
-
- Article
- Export citation
CENTRE OF BANACH ALGEBRA VALUED BEURLING ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2021, pp. 490-498
-
- Article
- Export citation
REVISITING THE RECTANGULAR CONSTANT IN BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2021, pp. 124-133
-
- Article
-
- You have access
- Open access
- Export citation
A FAMILY OF
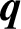 $\boldsymbol {q}$
-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$
-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
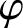 $\varphi $
-AMENABILITY OF DUAL BANACH ALGEBRAS
$\varphi $
-AMENABILITY OF DUAL BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 303-313
-
- Article
- Export citation
THE BOCHNER–SCHOENBERG-EBERLEIN PROPERTY OF EXTENSIONS OF BANACH ALGEBRAS AND BANACH MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 134-145
-
- Article
- Export citation
A NOTE ON OPEN BOOK EMBEDDINGS OF
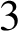 $3$
-MANIFOLDS IN
$3$
-MANIFOLDS IN
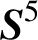 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2021, pp. 499-506
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
INTERSECTION OF CONJUGATE SOLVABLE SUBGROUPS IN FINITE CLASSICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2022, pp. 507-510
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
APPROXIMATELY MULTIPLICATIVE DECOMPOSITIONS OF NUCLEAR MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2021, pp. 314-322
-
- Article
- Export citation
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2021, pp. 146-153
-
- Article
-
- You have access
- Open access
- Export citation
NOTES ON ORTHOGONAL-COMPLETE METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 154-160
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
MODEL-BASED ADAPTIVE MONITORING: IMPROVING THE EFFECTIVENESS OF REEF MONITORING PROGRAMS
- Part of:
-
- Published online by Cambridge University Press:
- 09 February 2022, pp. 511-513
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
MANY FINITE-DIMENSIONAL LIFTING BUNDLE GERBES ARE TORSION
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2021, pp. 323-338
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
INTERACTING QUARTER-PLANE LATTICE WALK PROBLEMS: SOLUTIONS AND PROOFS
- Part of:
-
- Published online by Cambridge University Press:
- 05 November 2021, pp. 339-340
-
- Article
-
- You have access
- HTML
- Export citation
ADVERSARIAL RISK ANALYSIS FOR FIRST-PRICE SEALED-BID AUCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 514-515
-
- Article
-
- You have access
- HTML
- Export citation
CONFIDENCE INTERVALS IN GENERAL REGRESSION MODELS THAT UTILISE UNCERTAIN PRIOR INFORMATION
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 516-517
-
- Article
-
- You have access
- HTML
- Export citation
STATISTICAL STABILITY FOR DETERMINISTIC AND RANDOM DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 171-172
-
- Article
-
- You have access
- HTML
- Export citation
ON MAXIMAL SUBGROUPS OF IDEMPOTENT-GENERATED SEMIGROUPS ASSOCIATED WITH BIORDERED SETS
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2022, pp. 341-343
-
- Article
-
- You have access
- HTML
- Export citation