No CrossRef data available.
Article contents
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
Published online by Cambridge University Press: 16 April 2021
Abstract
Let A and
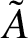 $\tilde A$
be unbounded linear operators on a Hilbert space. We consider the following problem. Let the spectrum of A lie in some horizontal strip. In which strip does the spectrum of
$\tilde A$
be unbounded linear operators on a Hilbert space. We consider the following problem. Let the spectrum of A lie in some horizontal strip. In which strip does the spectrum of
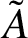 $\tilde A$
lie, if A and
$\tilde A$
lie, if A and
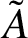 $\tilde A$
are sufficiently ‘close’? We derive a sharp bound for the strip containing the spectrum of
$\tilde A$
are sufficiently ‘close’? We derive a sharp bound for the strip containing the spectrum of
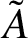 $\tilde A$
, assuming that
$\tilde A$
, assuming that
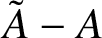 $\tilde A-A$
is a bounded operator and A has a bounded Hermitian component. We also discuss applications of our results to regular matrix differential operators.
$\tilde A-A$
is a bounded operator and A has a bounded Hermitian component. We also discuss applications of our results to regular matrix differential operators.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 146 - 153
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © Australian Mathematical Publishing Association Inc. 2021



