Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T17:33:23.183Z Has data issue: false hasContentIssue false
  • English
  • Français

REVISITING THE RECTANGULAR CONSTANT IN BANACH SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  26 April 2021

M. BARONTI Open the ORCID record for M. BARONTI [Opens in a new window] ,
E. CASINI Open the ORCID record for E. CASINI [Opens in a new window]  and
P. L. PAPINI Open the ORCID record for P. L. PAPINI [Opens in a new window]
M. BARONTI*
Affiliation:
Dipartimento di Matematica, Università di Genova, Via Dodecaneso 35, 16100 Genova, Italy
E. CASINI
Affiliation:
Dipartimento di Scienza e Alta Tecnologia, Università dell’Insubria, Via Valleggio 11, 22100 Como, Italy e-mail: [email protected]
P. L. PAPINI
Affiliation:
Via Martucci 19, 40136 Bologna, Italy e-mail: [email protected]
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a real Banach space. The rectangular constant 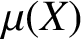$\mu (X)$ and some generalisations of it, 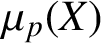$\mu _p(X)$ for 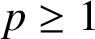$p \geq 1$ , were introduced by Gastinel and Joly around half a century ago. In this paper we make precise some characterisations of inner product spaces by using 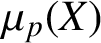$\mu _p(X)$ , correcting some statements appearing in the literature, and extend to 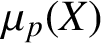$\mu _p(X)$ some characterisations of uniformly nonsquare spaces, known only for 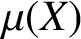$\mu (X)$ . We also give a characterisation of two-dimensional spaces with hexagonal norms. Finally, we indicate some new upper estimates concerning 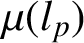$\mu (l_p)$ and 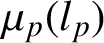$\mu _p(l_p)$ .

Keywords

hexagonal normorthogonal vectorsrectangular constantuniform nonsquareness

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B45: Banach sequence spaces 46B99: None of the above, but in this section 46C15: Characterizations of Hilbert spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 124 - 133
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Australian Mathematical Publishing Association Inc. 2021

References

Baronti, M., ‘On some parameters of normed spaces’, Boll. Unione Mat. Ital. B (5) 18(3) (1981), 1065–1085.Google Scholar
Beauzamy, B., Introduction to Banach Spaces and their Geometry , 2nd edn, North-Holland Mathematics Studies, 68 (North-Holland, Amsterdam, 1985).Google Scholar
Bynum, W. L., ‘Weak parallelogram laws for Banach spaces’, Canad. Math. Bull. 19(3) (1976), 269–275.CrossRefGoogle Scholar
del Río, M. and Benítez, C., ‘The rectangular constant for two-dimensional spaces’, J. Approx. Theory 19(1) (1977), 15–21.CrossRefGoogle Scholar
Desbiens, J., ‘Constante rectangle et biais d’un espace de Banach’, Bull. Aust. Math. Soc. 42(3) (1990), 465–482.CrossRefGoogle Scholar
Gastinel, N. and Joly, J. L., ‘Condition numbers and general projection method’, Linear Algebra Appl. 3 (1970), 185–224.CrossRefGoogle Scholar
James, R. C., ‘Orthogonality and linear functionals in normed linear spaces’, Trans. Amer. Math. Soc. 61 (1947), 265–292.CrossRefGoogle Scholar
Joly, J. L., ‘Caractérisations d’espaces hilbertiens au moyen de la constante rectangle’, J. Approx. Theory 2 (1969), 301–311.CrossRefGoogle Scholar
Joly, J. L., ‘La constante rectangle d’un espace vectoriel normé’, C. R. Acad. Sci. Paris Sér. A–B 268 (1969), A36–A38.Google Scholar
Paul, K., Ghosh, P. and Sain, D., ‘On rectangular constant in normed linear spaces’, J. Convex Anal. 24(3) (2017), 917–925.Google Scholar