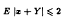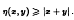Research Article
On optimal symmetric orthogonalisation and square roots of a normal matrix
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-246
-
- Article
-
- You have access
- Export citation
Multipliers on spaces of functions on compact groups with p-summable Fourier transforms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 435-442
-
- Article
-
- You have access
- Export citation
Posets, near unanimity functions and zigzags
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-93
-
- Article
-
- You have access
- Export citation
On the generalised Ruscheweyh class of analytic functions of complex order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-257
-
- Article
-
- You have access
- Export citation
Projectivity and duality in a Morita context
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 95-100
-
- Article
-
- You have access
- Export citation
On locally Lipschitz vector-valued invex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-272
-
- Article
-
- You have access
- Export citation
The approximate subdifferential of composite functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-455
-
- Article
-
- You have access
- Export citation
A decision problem for varieties of commutative semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 457-464
-
- Article
-
- You have access
- Export citation
Critical point theorems with relaxed boundary condition and applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-118
-
- Article
-
- You have access
- Export citation
Asymptotically stable stationary solutions to the reaction-diffusion equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-286
-
- Article
-
- You have access
- Export citation
On prime essential rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 287-290
-
- Article
-
- You have access
- Export citation
Subdifferentials are locally maximal monotone
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-471
-
- Article
-
- You have access
- Export citation
Ultrabornological Bochner integrable function spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 119-126
-
- Article
-
- You have access
- Export citation
Eigenvalue estimates and isoperimetric inequalities for cone-manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-143
-
- Article
-
- You have access
- Export citation
On relations between Jacobians and resultants of polynomials in two variables
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 473-481
-
- Article
-
- You have access
- Export citation
On skew-commuting mappings of rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-296
-
- Article
-
- You have access
- Export citation
Biconcave-function characterisations of UMD and Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 297-306
-
- Article
-
- You have access
- Export citation
A minimax inequality with applications to existence of equilibrium points
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 483-503
-
- Article
-
- You have access
- Export citation
Embedding up to homotopy type in Euclidean space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-148
-
- Article
-
- You have access
- Export citation
Strictly real Banach algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 505-519
-
- Article
-
- You have access
- Export citation

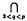 (
(