Article contents
Biconcave-function characterisations of UMD and Hilbert spaces
Published online by Cambridge University Press: 17 April 2009
Abstract
Suppose that X is a real or complex Banach space with norm |·|. Then X is a Hilbert space if and only if
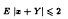
for all x in X and all X-valued Bochner integrable functions Y on the Lebesgue unit interval satisfying EY = 0 and |x − Y| ≤ 2 almost everywhere. This leads to the following biconcave-function characterisation: A Banach space X is a Hilbert space if and only if there is a biconcave function η: {(x, y) ∈ X × X: |x − y| ≤ 2} → R such that η(0, 0) = 2 and
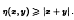
If the condition η(0, 0) = 2 is eliminated, then the existence of such a function η characterises the class UMD (Banach spaces with the unconditionally property for martingale differences).
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1993
References
- 1
- Cited by


