Research Article
Axioms for convexity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 179-197
-
- Article
-
- You have access
- Export citation
Pure subgroups of LCA groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 199-204
-
- Article
-
- You have access
- Export citation
Locally Lipschitz functions are generically pseudo-regular on separable Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 205-212
-
- Article
-
- You have access
- Export citation
A characterisation of compact minimal hypersurfaces in a unit sphere
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-216
-
- Article
-
- You have access
- Export citation
Equationally defined radical classes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 217-220
-
- Article
-
- You have access
- Export citation
Socles of Verma modules in quantum groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-231
-
- Article
-
- You have access
- Export citation
On optimal symmetric orthogonalisation and square roots of a normal matrix
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-246
-
- Article
-
- You have access
- Export citation
On the generalised Ruscheweyh class of analytic functions of complex order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-257
-
- Article
-
- You have access
- Export citation
On locally Lipschitz vector-valued invex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-272
-
- Article
-
- You have access
- Export citation
Asymptotically stable stationary solutions to the reaction-diffusion equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-286
-
- Article
-
- You have access
- Export citation
On prime essential rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 287-290
-
- Article
-
- You have access
- Export citation
On skew-commuting mappings of rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-296
-
- Article
-
- You have access
- Export citation
Biconcave-function characterisations of UMD and Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 297-306
-
- Article
-
- You have access
- Export citation
Small zeros of quadratic L-functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-319
-
- Article
-
- You have access
- Export citation
On union-closed sets and Conway's sequence
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-332
-
- Article
-
- You have access
- Export citation
A formula on the subdifferential of the deconvolution of convex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 333-340
-
- Article
-
- You have access
- Export citation
Further results on the deficiencies of algebroid functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 341-346
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Continuity conditions defined by indices of non-compactness and applications to differentiability theory
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 347-348
-
- Article
-
- You have access
- Export citation
Metacyclic groups of odd order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 349-350
-
- Article
-
- You have access
- Export citation
Maximal functions and harmonic analysis
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 351
-
- Article
-
- You have access
- Export citation

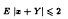
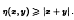
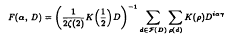
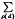 denotes the sum over the non-trivial zeros
denotes the sum over the non-trivial zeros 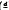 ) is the Kronecker symbol. The outer sum
) is the Kronecker symbol. The outer sum 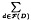 is over all fundamental discriminants
is over all fundamental discriminants