Research Article
Annihilator graphs and semigroups of matrices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
On some sub-Riemannian objects in hypersurfaces of sub-Riemannian manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-198
-
- Article
-
- You have access
- Export citation
On finite G-locally primitive graphs and the Weiss conjecture
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-356
-
- Article
-
- You have access
- Export citation
On generalised mixed co-quasi-variational inequalities with noncompact valued mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 7-15
-
- Article
-
- You have access
- Export citation
Direct products and properly 3-realisable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 199-205
-
- Article
-
- You have access
- Export citation
Maximal averages along curves over the p-adic numbers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-375
-
- Article
-
- You have access
- Export citation
ABS-type methods for solving full row rank linear systems using a new rank two update
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 17-34
-
- Article
-
- You have access
- Export citation
Pointed Blaschke manifolds and geodesic normal sections
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-383
-
- Article
-
- You have access
- Export citation
A proof of Higgins's conjecture
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-212
-
- Article
-
- You have access
- Export citation
The curvature and topological properties of hypersurfaces with constant scalar curvature
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 35-44
-
- Article
-
- You have access
- Export citation
The similarity problem for tensor products of certain C*-algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 385-389
-
- Article
-
- You have access
- Export citation
On evaluation formulas for double L-values
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-221
-
- Article
-
- You have access
- Export citation
On hypercyclicity and supercyclicity criteria
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-54
-
- Article
-
- You have access
- Export citation
On the orders of generators of capable p-groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-395
-
- Article
-
- You have access
- Export citation
Complementation in the group of units of matrix rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 223-227
-
- Article
-
- You have access
- Export citation
A remark on preinvex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 397-400
-
- Article
-
- You have access
- Export citation
Fixed point property for general topologies in some Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 229-244
-
- Article
-
- You have access
- Export citation
A Riemannian invariant and its applications to Einstein manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-65
-
- Article
-
- You have access
- Export citation
On the injectivity of the Vassiliev homomorphism of singular Artin monoids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 401-422
-
- Article
-
- You have access
- Export citation
Rolling of a body on a plane or a sphere: a geometric point of view
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-256
-
- Article
-
- You have access
- Export citation

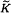
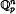 defined by
defined by 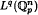 bounded, where 1 <
bounded, where 1 < 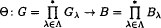 be a group homomorphism between free products of groups such that
be a group homomorphism between free products of groups such that 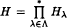 such that
such that 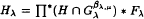 where
where 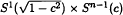 , where
, where