Research Article
Twisted Alexander polynomial for the Lawrence-Krammer representation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-71
-
- Article
-
- You have access
- Export citation
Non-minimal tree actions and the existence of non-uniform tree lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 257-266
-
- Article
-
- You have access
- Export citation
Two necessary and sufficient conditions for Möbius subgroups to be g-discontinuous
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 423-427
-
- Article
-
- You have access
- Export citation
Pseudo-differential equations connected with p-adic forms and local zeta functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 73-86
-
- Article
-
- You have access
- Export citation
The class groups of the imaginary Abelian number fields with Galois group (ℤ/2ℤ)n
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-277
-
- Article
-
- You have access
- Export citation
Characterisation of the sub-Riemannian isometry groups of the H-type groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 87-100
-
- Article
-
- You have access
- Export citation
Existence and L∞ estimates for a class of singular ordinary differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-440
-
- Article
-
- You have access
- Export citation
Polynomial near-rings in k indeterminates
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-449
-
- Article
-
- You have access
- Export citation
Topological entropy for the canonical completely positive maps on graph C*-Algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-116
-
- Article
-
- You have access
- Export citation
On two open problems about strongly clean rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-282
-
- Article
-
- You have access
- Export citation
Blocks of consecutive integers in sumsets (A + B)t
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 283-291
-
- Article
-
- You have access
- Export citation
Quadratic reverses of the triangle inequality for Bochner integral in Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-462
-
- Article
-
- You have access
- Export citation
Polynomials on banach spaces whose duals are isomorphic to ℓ1 (Γ)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-124
-
- Article
-
- You have access
- Export citation
Norm of composition operators on the Bloch space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-299
-
- Article
-
- You have access
- Export citation
Trace of Frobenius endomorphism of an elliptic curve with complex multiplication
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 125-142
-
- Article
-
- You have access
- Export citation
Diametrically contractive mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 463-468
-
- Article
-
- You have access
- Export citation
A counterexample using 4-linear forms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-473
-
- Article
-
- You have access
- Export citation
Riemannian manifolds whose curvature operator R(X, Y) has constant eigenvalues
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 301-319
-
- Article
-
- You have access
- Export citation
Classification theorems for the C*-Algebras of graphs with sinks
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 143-161
-
- Article
-
- You have access
- Export citation
On τ-completely decomposable modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 163-175
-
- Article
-
- You have access
- Export citation

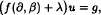 where
where 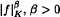 ,
, 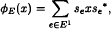 then Voiculescu's topological entropy ht(φ
then Voiculescu's topological entropy ht(φ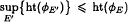 , where the supremum is taken over the set of all finite subgraphs of
, where the supremum is taken over the set of all finite subgraphs of