Research Article
A note on Lagrange interpolation for |x|λ at equidistant nodes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-480
-
- Article
-
- You have access
- Export citation
Prediction of fractional Brownian motion with Hurst index less than 1/2
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-328
-
- Article
-
- You have access
- Export citation
Abelian groups as inner mapping groups of loops
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 481-488
-
- Article
-
- You have access
- Export citation
Distance to the intersection of two sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-341
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 70 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
A note on a continued fraction of Ramanujan
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 489-497
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 70 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Invariant analytic hypersurfaces in complex Lie groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 343-349
-
- Article
-
- You have access
- Export citation
Witt kernels of bi-quadratic extensions in characteristic 2: Addendum
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 351
-
- Article
-
- You have access
- Export citation
Stability of Dhombres' equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-505
-
- Article
-
- You have access
- Export citation
Properly embedded and immersed minimal surfaces in the Heisenberg group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 507-520
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 70 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Hardy-type inequalities for means
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-528
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 70 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Index
Bulletin of the Australian Mathematical Society Author Index, Volume 61 (2000) – 70 (2004)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 529-561
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 70 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 70 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

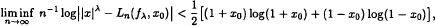 where λ > 0, λ ≠ 2, 4, … and
where λ > 0, λ ≠ 2, 4, … and 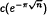 for various positive integers
for various positive integers 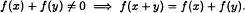 This paper is devoted to the stability of the above equation.
This paper is devoted to the stability of the above equation.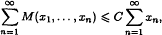 ,
Where
,
Where