Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-09T15:47:03.783Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct products and properly 3-realisable groups

Published online by Cambridge University Press:  17 April 2009

Manuel Cárdenas ,
Francisco F. Lasheras  and
Ranja Roy
Manuel Cárdenas
Affiliation:
Departamento de Geometría y Topología, Universidad de Sevilla, Apdo 1160, 41080-Sevilla, Spain e-mail: [email protected], [email protected]
Francisco F. Lasheras
Affiliation:
Departamento de Geometría y Topología, Universidad de Sevilla, Apdo 1160, 41080-Sevilla, Spain e-mail: [email protected], [email protected]
Ranja Roy
Affiliation:
New York Institute of Technology, Old Westbury, NY 11568–8000, United States of America e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we show that the direct of infinite finitely presented groups is always properly 3-realisable. We also show that classical hyperbolic groups are properly 3-realisable. We recall that a finitely presented group G is said to be properly 3-realisable if there exists a compact 2-polyhedron K with π1 (K) ≅ G and whose universal cover 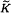has the proper homotopy type of a (p.1.) 3-manifold with boundary. The question whether or not every finitely presented is properly 3-realisable remains open.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 70 , Issue 2 , October 2004 , pp. 199 - 205
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Ayala, R., Cárdenas, M., Lasheras, F.F. and Quintero, A., ‘Properly 3-realizable groups’, Proc. Amer. Math. Soc. (to appear).Google Scholar
[2]Baues, H-J. and Quintero, A., Infinite homotopy theory, K-monographs in Mathematics 6 (Kluwer Academic Publishers, Dordrecht, 2001).Google Scholar
[3]Brown, R., Elements of modern topology (McGraw-Hill, New York, 1968).Google Scholar
[4]Cárdenas, M., Fernández, T., Lasheras, F. F. and Quintero, A., ‘Embedding proper homotopy types’, Colloq. Math. 95 (2003), 1–20.CrossRefGoogle Scholar
[5]Cárdenas, M. and Lasheras, F.F., ‘On properly 3-realizable groups’, Topology Appl. (to appear).Google Scholar
[6]Cárdenas, M. and Lasheras, F.F., ‘Properly 3-realizable groups: a survey’, in Proceedings of the Conference on Geometric Group Theory and Geometric Methods in Group Theory (Seville 2003), Contemp. Math. (to appear).Google Scholar
[7]Cárdenas, M., Lasheras, F.F., Muro, F. and Quintero, A., ‘Proper L-S category, fundamental pro-groups and 2-dimensional proper co-H-spaces’, (preprint).Google Scholar
[8]Geoghegan, R. and Mihalik, M., ‘The fundamental group at infinity’, Topology 35 (1996), 655–669.CrossRefGoogle Scholar
[9]Lasheras, F.F., ‘Universal covers and 3-manifolds’, J. Pure Appl. Algebra 151 (2000), 163–172.CrossRefGoogle Scholar
[10]Lasheras, F.F., ‘A note on fake surfaces and universal covers’, Topology Appl. 125 (2002), 497–504.CrossRefGoogle Scholar
[11]Mardesic, S. and Segal, J., Shape theory, North-Holland Mathematical Library 26 (North-Holland, Amsterdam, New York 1982).Google Scholar
[12]May, P.J., A concise course in algebraic topology, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 1999).Google Scholar
[13]Mihalik, M., ‘Semistability at the end of a group extension’, Trans. Amer. Math. Soc. 277 (1983), 307–321.CrossRefGoogle Scholar
[14]Scott, P. and Wall, C.T.C., ‘Topological methods in group theory’, in Homological Group Theory, London Math. Soc. Lecture Notes (Cambridge Univ. Press 36, Cambridge, New York, 1979), pp. 137–204.CrossRefGoogle Scholar