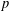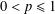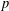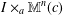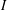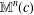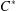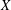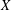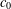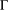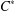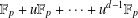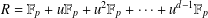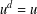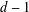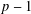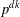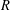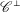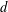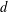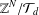Research Article
MAPPINGS OF CONSERVATIVE DISTANCES IN
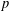 $p$-NORMED SPACES (
$p$-NORMED SPACES (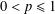 $0<p\leq 1$)
$0<p\leq 1$)
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 291-298
-
- Article
-
- You have access
- Export citation
AN ELEMENTARY PROOF OF JAMES’ CHARACTERISATION OF WEAK COMPACTNESS. II
- Part of:
-
- Published online by Cambridge University Press:
- 26 September 2016, pp. 133-137
-
- Article
-
- You have access
- Export citation
A DDVV INEQUALITY FOR SUBMANIFOLDS OF WARPED PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 495-499
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF CENTRAL ELEMENTS IN
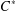 $C^{\ast }$ -ALGEBRAS
$C^{\ast }$ -ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 138-143
-
- Article
-
- You have access
- Export citation
COMPARING THE GENERALISED ROUNDNESS OF METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 299-314
-
- Article
-
- You have access
- Export citation
HAAGERUP PROPERTY FOR
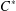 $C^{\ast }$ -CROSSED PRODUCTS
$C^{\ast }$ -CROSSED PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 144-148
-
- Article
-
- You have access
- Export citation
STRUCTURE TOPOLOGY AND EXTREME OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 315-321
-
- Article
-
- You have access
- Export citation
A NEW DERIVATIVE-FREE CONJUGATE GRADIENT METHOD FOR LARGE-SCALE NONLINEAR SYSTEMS OF EQUATIONS
-
- Published online by Cambridge University Press:
- 22 March 2017, pp. 500-511
-
- Article
-
- You have access
- Export citation
OPERATOR QUASILINEARITY OF SOME FUNCTIONALS ASSOCIATED WITH DAVIS–CHOI–JENSEN’S INEQUALITY FOR POSITIVE MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 322-332
-
- Article
-
- You have access
- Export citation
BEST PROXIMITY POINT THEOREMS FOR CYCLIC QUASI-CONTRACTION MAPS IN UNIFORMLY CONVEX BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2016, pp. 149-156
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
OBSTRUCTION THEORY FOR SUPERMANIFOLDS AND DEFORMATIONS OF SUPERCONFORMAL STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2017, pp. 512-514
-
- Article
-
- You have access
- Export citation
Research Article
ON THE SUPPORT WEIGHT DISTRIBUTION OF LINEAR CODES OVER THE RING
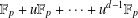 $\mathbb{F}_{p}+u\mathbb{F}_{p}+\cdots +u^{d-1}\mathbb{F}_{p}$
$\mathbb{F}_{p}+u\mathbb{F}_{p}+\cdots +u^{d-1}\mathbb{F}_{p}$
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 157-163
-
- Article
-
- You have access
- Export citation
A PURELY METRIC PROOF OF THE CARISTI FIXED POINT THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 333-337
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
HOLOMORPHIC FLEXIBILITY PROPERTIES OF SPACES OF ELLIPTIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, p. 515
-
- Article
-
- You have access
- Export citation
REGRESSION CLUSTERING USING GIBBS SAMPLER AND OPTIMAL CLUSTER NUMBER ESTIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 516-517
-
- Article
-
- You have access
- Export citation
Research Article
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
SKETCHES IN HIGHER CATEGORY THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 26 September 2016, p. 164
-
- Article
-
- You have access
- Export citation
A FEW FAMILIES OF CAYLEY GRAPHS AND THEIR EFFICIENCY AS COMMUNICATION NETWORKS
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 518-520
-
- Article
-
- You have access
- Export citation
TOPOLOGY OF COMPLEX NETWORKS: MODELS AND ANALYSIS
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 347-349
-
- Article
-
- You have access
- Export citation
ON ASPECTS OF NUMERICAL ERGODIC THEORY: STABILITY OF ULAM’S METHOD, COMPUTING OSELEDETS SUBSPACES AND OPTIMAL MIXING
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2016, pp. 165-166
-
- Article
-
- You have access
- Export citation