Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T16:46:03.406Z Has data issue: false hasContentIssue false
  • English
  • Français

A DDVV INEQUALITY FOR SUBMANIFOLDS OF WARPED PRODUCTS

Part of: Global differential geometry

Published online by Cambridge University Press:  05 January 2017

JULIEN ROTH
JULIEN ROTH*
Affiliation:
LAMA, UPEM-UPEC-CNRS, Cité Descartes, Champs sur Marne, 77454 Marne-la-Vallée cedex 2, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a DDVV inequality for submanifolds of warped products of the form 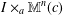$I\times _{a}\mathbb{M}^{n}(c)$ , where 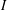$I$ is an interval and 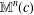$\mathbb{M}^{n}(c)$ is a real space form of curvature $c$ . As an application, we give a rigidity result for submanifolds of 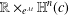$\mathbb{R}\times _{e^{\unicode[STIX]{x1D706}t}}\mathbb{H}^{n}(c)$ .

Keywords

warped productrigidityimmersion

MSC classification

Primary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Secondary: 53C24: Rigidity results
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 3 , June 2017 , pp. 495 - 499
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Chen, Q. and Cui, Q., ‘Normal scalar curvature and a pinching theorem in S m ×ℝ and ℍ m ×ℝ’, Sci. China Math. 54(9) (2011), 1977–1984.Google Scholar
De Smet, P. J., Dillen, F., Verstraelen, L. and Vrancken, L., ‘A pointwise inequality in submanifold theory’, Arch. Math. 35(1) (1999), 115–128.Google Scholar
Dillen, F., Fastenakels, J. and Van der Veken, J., ‘Remarks on an inequality involving the normal scalar curvature’, in: Pure and Applied Differential Geometry (Shaker, Aachen, 2007), 83–92.Google Scholar
Ge, J. Q. and Tang, Z. Z., ‘A proof of the DDVV conjecture and its equality case’, Pacific J. Math. 237 (2008), 87–95.Google Scholar
Lawn, M.-A. and Ortega, M., ‘A fundamental theorem for hypersurfaces in semi-Riemannian warped products’, J. Geom. Phys. 90 (2015), 55–70.CrossRefGoogle Scholar
Lu, Z. Q., ‘Normal scalar curvature conjecture and its applications’, J. Funct. Anal. 261 (2011), 1284–1308.Google Scholar