Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T04:10:02.626Z Has data issue: false hasContentIssue false
  • English
  • Français

STRUCTURE TOPOLOGY AND EXTREME OPERATORS

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  19 October 2016

ANA M. CABRERA-SERRANO  and
JUAN F. MENA-JURADO
ANA M. CABRERA-SERRANO
Affiliation:
Universidad de Granada, Facultad de Ciencias, Departamento de Análisis Matemático, 18071 Granada, Spain email [email protected]
JUAN F. MENA-JURADO*
Affiliation:
Universidad de Granada, Facultad de Ciencias, Departamento de Análisis Matemático, 18071 Granada, Spain email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

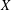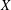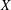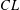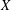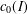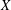We say that a Banach space $X$ is ‘nice’ if every extreme operator from any Banach space into $X$ is a nice operator (that is, its adjoint preserves extreme points). We prove that if $X$ is a nice almost $CL$-space, then $X$ is isometrically isomorphic to $c_{0}(I)$ for some set $I$. We also show that if $X$ is a nice Banach space whose closed unit ball has the Krein–Milman property, then 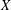$X$ is 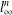$l_{\infty }^{n}$ for some 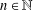$n\in \mathbb{N}$. The proof of our results relies on the structure topology.

Keywords

extreme operatorstructure topologyalmost CL-spaceBanach space

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B04: Isometric theory of Banach spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 315 - 321
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

Supported by Spanish MINECO and FEDER projects Nos MTM2012-31755 and MTM2015-65020-P and by Junta de Andalucía and FEDER Grant FQM-185.

References

Alfsen, E. M. and Effros, E. G., ‘Structure in real Banach spaces II’, Ann. of Math. 96 (1972), 129–173.CrossRefGoogle Scholar
Blumenthal, R. M., Lindenstrauss, J. and Phelps, R. R., ‘Extreme operators into C (K)’, Pacific J. Math. 15 (1965), 747–756.Google Scholar
Cabrera-Serrano, A. M. and Mena-Jurado, J. F., ‘On extreme operators whose adjoints preserve extreme points’, J. Convex Anal. 22 (2015), 247–258.Google Scholar
Cabrera-Serrano, A. M. and Mena-Jurado, J. F., ‘Facial topology and extreme operators’, J. Math. Anal. Appl. 427 (2015), 899–904.Google Scholar
Cabrera-Serrano, A. M. and Mena-Jurado, J. F., ‘Nice operators into G-spaces’, Bull. Malays. Math. Sci. Soc. to appear, doi:10.1007/s40840-015-0155-8.Google Scholar
Diestel, J. and Uhl, J. J., Vector Measures, Mathematical Surveys, 15 (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos Santalucía, V., Pelant, J. and Zizler, V., Functional Analysis and Infinite-Dimensional Geometry (Springer, New York, 2001).CrossRefGoogle Scholar
Fullerton, R. E., ‘Geometrical characterizations of certain function spaces’, in: Proc. Int. Symp. Linear Spaces (Jerusalem, 1960) (Jerusalem Academic Press–Pergamon Press, Jerusalem–Oxford, 1961), 227–236.Google Scholar
Harmand, P., Werner, D. and Werner, W., M-Ideals in Banach Spaces and Banach Algebras, Lecture Notes in Mathematics, 1547 (Springer, Berlin, 1993).Google Scholar
Lima, Å., ‘Intersection properties of balls and subspaces in Banach spaces’, Trans. Amer. Math. Soc. 227 (1977), 1–62.CrossRefGoogle Scholar
Lima, Å., ‘Intersection properties of balls in spaces of compact operators’, Ann. Inst. Fourier (Grenoble) 28 (1978), 35–65.Google Scholar
Lindenstrauss, J., ‘Extensions of compact operators’, Mem. Amer. Math. Soc. No. 48 (1964).CrossRefGoogle Scholar
Martín, M., ‘Banach spaces having the Radon–Nikodỳm property and numerical index 1’, Proc. Amer. Math. Soc. 131 (2003), 3407–3410.CrossRefGoogle Scholar
Martín, M. and Payá, R., ‘On CL-spaces and almost CL-spaces’, Ark. Mat. 42 (2004), 107–118.Google Scholar
Morris, P. D. and Phelps, R. R., ‘Theorems of Krein–Milman type for certain convex sets of operators’, Trans. Amer. Math. Soc. 150 (1970), 183–200.Google Scholar
Navarro-Pascual, J. C. and Navarro, M. A., ‘Nice operators and surjective isometries’, J. Math. Anal. Appl. 426 (2015), 1130–1142.Google Scholar
Navarro-Pascual, J. C. and Navarro, M. A., ‘Differentiable functions and nice operators’, Banach J. Math. Anal. 10 (2016), 96–107.Google Scholar
Sharir, M., ‘Extremal structure in operator spaces’, Trans. Amer. Math. Soc. 186 (1973), 91–111.Google Scholar
Sharir, M., ‘A counterexample on extreme operators’, Israel J. Math. 24 (1976), 320–337.Google Scholar
Sharir, M., ‘A non-nice extreme operator’, Israel J. Math. 26 (1977), 306–312.Google Scholar