Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T15:08:57.800Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH

Part of: Abelian groups Discrete geometry Elementary number theory Forms and linear algebraic groups

Published online by Cambridge University Press:  02 November 2016

KRZYSZTOF KOŁODZIEJCZYK  and
RAFAŁ SAŁAPATA
KRZYSZTOF KOŁODZIEJCZYK*
Affiliation:
Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland email [email protected]
RAFAŁ SAŁAPATA
Affiliation:
Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A lattice walk with all steps having the same length 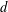$d$ is called a 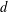$d$-walk. Denote by 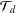${\mathcal{T}}_{d}$ the terminal set, that is, the set of all lattice points that can be reached from the origin by means of a 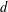$d$-walk. We examine some geometric and algebraic properties of the terminal set. After observing that 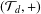$({\mathcal{T}}_{d},+)$ is a normal subgroup of the group 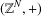$(\mathbb{Z}^{N},+)$, we ask questions about the quotient group 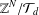$\mathbb{Z}^{N}/{\mathcal{T}}_{d}$ and give the number of elements of 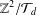$\mathbb{Z}^{2}/{\mathcal{T}}_{d}$ in terms of 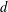$d$. To establish this result, we use several consequences of Fermat’s theorem about representations of prime numbers of the form 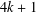$4k+1$ as the sum of two squares. One of the consequences is the fact, observed by Sierpiński, that every natural power of such a prime number has exactly one relatively prime representation. We provide explicit formulas for the relatively prime integers in this representation.

Keywords

lattice d-walkterminal setsublatticequotient groupprime numbersum of squares

MSC classification

Primary: 52C05: Lattices and convex bodies in $2$ dimensions
Secondary: 11A41: Primes 11E25: Sums of squares and representations by other particular quadratic forms 20K27: Subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 338 - 346
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author has been partially supported by NCN grant No. 2014/15/B/ST1/00166.

References

Banderier, C. and Flajolet, Ph., ‘Basic analytic combinatorics of directed lattice paths’, Theoret. Comput. Sci. 281 (2002), 37–80.Google Scholar
Burton, D. M., Elementary Number Theory (McGraw-Hill, Boston, 2002).Google Scholar
Dabbagian-Abdoly, V., ‘On the enumeration of higher dimensional lattice paths’, Int. J. Pure Appl. Math. 23 (2005), 475–477.Google Scholar
De Loera, J. A., Hemmecke, R. and Köppe, M., Algebraic and Geometric Ideas in the Theory of Discrete Optimization, MOS-SIAM Series on Optimization (SIAM, Philadelphia, 2013).Google Scholar
Dickson, L. E., History of the Theory of Numbers, Vol. 2 (Carnegie Institution of Washington, 1920), republished by Dover, New York, 2005.Google Scholar
Jensen, I., ‘Enumeration of self-avoiding walks on the square lattice’, J. Phys. A 37 (2004), 5503–5524.Google Scholar
Kołodziejczyk, K., ‘Parity properties and terminal points for lattice walks with steps of equal length’, J. Math. Anal. Appl. 35 (2009), 363–368.Google Scholar
Sierpiński, W., ‘Sur les nombres impairs admettant une seule décomposition en une somme de deux carrés de nombres naturels premiers entre eux’, Elem. Math. 16 (1961), 27–30.Google Scholar
Sierpiński, W., Elementary Theory of Numbers (ed. Schinzel, A.) (North-Holland, Amsterdam, 1988).Google Scholar
Tamm, U., ‘Lattice paths not touching a given boundary’, J. Statist. Plann. Inference 105 (2002), 433–448.CrossRefGoogle Scholar
Woan, W.-J., ‘Diagonal lattice paths’, Congr. Numer. 151 (2001), 173–178.Google Scholar