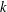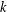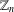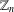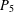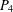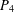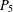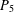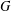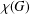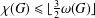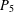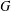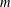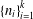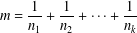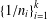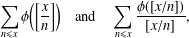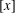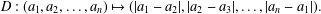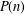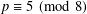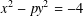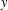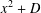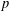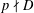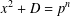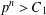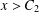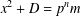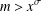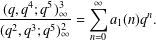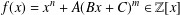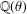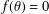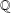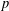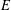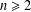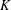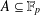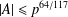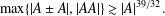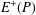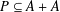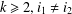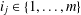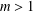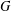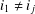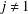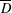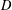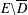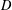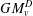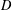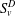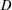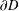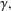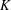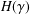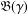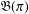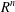Research Article
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
-
- Article
-
- You have access
- Export citation
A BOUND FOR THE CHROMATIC NUMBER OF (
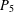 $P_{5}$, GEM)-FREE GRAPHS
$P_{5}$, GEM)-FREE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2019, pp. 182-188
-
- Article
-
- You have access
- Export citation
A NOTE ON THE SUM OF RECIPROCALS
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 189-193
-
- Article
-
- You have access
- Export citation
NOTE ON SUMS INVOLVING THE EULER FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 194-200
-
- Article
-
- You have access
- Export citation
PERIODS OF DUCCI SEQUENCES AND ODD SOLUTIONS TO A PELLIAN EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 201-205
-
- Article
-
- You have access
- Open access
- Export citation
ON THE FACTORISATION OF
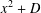 $x^{2}+D$
$x^{2}+D$
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2019, pp. 206-215
-
- Article
-
- You have access
- Export citation
VANISHING COEFFICIENTS IN FOUR QUOTIENTS OF INFINITE PRODUCT EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 216-224
-
- Article
-
- You have access
- Export citation
A LOWER BOUND FOR THE LARGE SIEVE WITH SQUARE MODULI
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 225-229
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE RANK STATISTIC FOR STRONGLY CONCAVE COMPOSITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 230-238
-
- Article
-
- You have access
- Export citation
A BRIEF NOTE ON SOME INFINITE FAMILIES OF MONOGENIC POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 239-244
-
- Article
-
- You have access
- Export citation
ON THE SELMER GROUP OF A CERTAIN
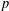 $p$-ADIC LIE EXTENSION
$p$-ADIC LIE EXTENSION
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 245-255
-
- Article
-
- You have access
- Export citation
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2019, pp. 256-267
-
- Article
-
- You have access
- Export citation
A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2019, pp. 268-280
-
- Article
-
- You have access
- Export citation
A NILPOTENCY CRITERION FOR SOME VERBAL SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 281-289
-
- Article
-
- You have access
- Export citation
A NOTE ON THE PERIODICITY OF ENTIRE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 290-296
-
- Article
-
- You have access
- Export citation
EXTENDABLE TEMPERATURES
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 297-303
-
- Article
-
- You have access
- Export citation
A SYSTEM OF FUNCTIONAL EQUATIONS SATISFIED BY COMPONENTS OF A QUADRATIC FUNCTION AND ITS STABILITY
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 304-316
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE FROBENIUS RECIPROCITY THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2019, pp. 317-322
-
- Article
-
- You have access
- Export citation
A NOTE ON RADIAL SYMMETRY FOR AN INTEGRAL EQUATION OF WOLFF TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2019, pp. 323-327
-
- Article
-
- You have access
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
-
- Article
-
- You have access
- Export citation