Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T11:16:21.849Z Has data issue: false hasContentIssue false
  • English
  • Français

VANISHING COEFFICIENTS IN FOUR QUOTIENTS OF INFINITE PRODUCT EXPANSIONS

Part of: Discontinuous groups and automorphic forms Series expansions

Published online by Cambridge University Press:  20 March 2019

DAZHAO TANG
DAZHAO TANG*
Affiliation:
College of Mathematics and Statistics, Chongqing University, Huxi Campus LD204, Chongqing 401331, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by Ramanujan’s continued fraction and the work of Richmond and Szekeres [‘The Taylor coefficients of certain infinite products’, Acta Sci. Math. (Szeged)40(3–4) (1978), 347–369], we investigate vanishing coefficients along arithmetic progressions in four quotients of infinite product expansions and obtain similar results. For example, 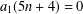$a_{1}(5n+4)=0$, where 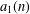$a_{1}(n)$ is defined by

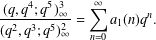$$\begin{eqnarray}\displaystyle {\displaystyle \frac{(q,q^{4};q^{5})_{\infty }^{3}}{(q^{2},q^{3};q^{5})_{\infty }^{2}}}=\mathop{\sum }_{n=0}^{\infty }a_{1}(n)q^{n}. & & \displaystyle \nonumber\end{eqnarray}$$

Keywords

vanishing coefficientsquotients of infinite productJacobi’s triple product identityquintuple product identity

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 30B10: Power series (including lacunary series)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 216 - 224
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Natural Science Foundation of China (No. 11501061) and the Fundamental Research Funds for the Central Universities (No. 2018CDXYST0024).

References

Alladi, K. and Gordon, B., ‘Vanishing coefficients in the expansion of products of Rogers–Ramanujan type’, in: Proc. Rademacher Centenary Conf., Contemporary Mathematics, 166 (eds. Andrews, G. E. and Bressoud, D.) (American Mathematical Society, Providence, RI, 1994), 129–139.Google Scholar
Andrews, G. E., ‘Ramanujan’s “lost” notebook III. The Rogers–Ramanujan continued fraction’, Adv. Math. 41 (1981), 186–208.10.1016/0001-8708(81)90015-3Google Scholar
Andrews, G. E. and Bressoud, D. M., ‘Vanishing coefficients in infinite product expansions’, J. Aust. Math. Soc. Ser. A 27(2) (1979), 199–202.Google Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).Google Scholar
Hirschhorn, M. D., ‘On the expansion of Ramanujan’s continued fraction’, Ramanujan J. 5 (1998), 521–527.10.1023/A:1009789012006Google Scholar
Hirschhorn, M. D., ‘Two remarkable q-series expansions’, Ramanujan J., to appear, doi:10.1007/s11139-018-0016-9.Google Scholar
Hirschhorn, M. D., The Power of q , Developments in Mathematics, 49 (Springer, Cham, 2017).Google Scholar
McLaughlin, J., ‘Further results on vanishing coefficients in infinite product expansions’, J. Aust. Math. Soc. Ser. A 98 (2015), 69–77.Google Scholar
Richmond, B. and Szekeres, G., ‘The Taylor coefficients of certain infinite products’, Acta Sci. Math. (Szeged) 40(3–4) (1978), 347–369.Google Scholar
Tang, D., ‘Vanishing coefficients in some q-series expansions’, Int. J. Number Theory, to appear, doi:10.1142/S1793042119500398.Google Scholar