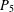Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T01:33:13.739Z Has data issue: false hasContentIssue false
  • English
  • Français

A BOUND FOR THE CHROMATIC NUMBER OF ($P_{5}$, GEM)-FREE GRAPHS

Part of: Discrete mathematics in relation to computer science Graph theory

Published online by Cambridge University Press:  28 March 2019

KATHIE CAMERON Open the ORCID record for KATHIE CAMERON [Opens in a new window] ,
SHENWEI HUANG Open the ORCID record for SHENWEI HUANG [Opens in a new window]  and
OWEN MERKEL Open the ORCID record for OWEN MERKEL [Opens in a new window]
KATHIE CAMERON
Affiliation:
Department of Mathematics, Wilfrid Laurier University, Waterloo, ON, Canada N2L 3C5 email [email protected]
SHENWEI HUANG*
Affiliation:
College of Computer Science, Nankai University, Tianjin 300350, China email [email protected]
OWEN MERKEL
Affiliation:
David R. Cheriton School of Computer Science, University of Waterloo, Waterloo, ON, Canada N2L 3G1 email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As usual, 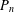$P_{n}$ (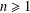$n\geq 1$) denotes the path on $n$ vertices. The gem is the graph consisting of a 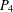$P_{4}$ together with an additional vertex adjacent to each vertex of the 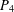$P_{4}$. A graph is called (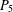$P_{5}$, gem)-free if it has no induced subgraph isomorphic to a 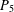$P_{5}$ or to a gem. For a graph 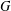$G$, 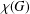$\unicode[STIX]{x1D712}(G)$ denotes its chromatic number and 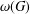$\unicode[STIX]{x1D714}(G)$ denotes the maximum size of a clique in 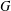$G$. We show that 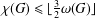$\unicode[STIX]{x1D712}(G)\leq \lfloor \frac{3}{2}\unicode[STIX]{x1D714}(G)\rfloor$ for every (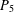$P_{5}$, gem)-free graph 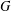$G$.

Keywords

graph colouringhereditary classeschi-bound

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C75: Structural characterization of families of graphs 05C85: Graph algorithms 68R10: Graph theory (including graph drawing)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 182 - 188
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

Shenwei Huang is the corresponding author. The research of the first author was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) grant RGPIN-2016-06517; the research of the second author was supported by the National Natural Science Foundation of China grant 11801284; the research of the third author was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) grant RGPIN-2016-06517 and an NSERC Undergraduate Student Research Award.

References

Brandstädt, A. and Kratsch, D., ‘On the structure of (P 5 , gem)-free graphs’, Discrete Appl. Math. 145(2) (2005), 155–166.Google Scholar
Choudum, S. A., Karthick, T. and Shalu, M. A., ‘Perfect coloring and linearly 𝜒-bound P 6 -free graphs’, J. Graph Theory 54(4) (2007), 293–306.Google Scholar
Chudnovsky, M. and Sivaraman, V., ‘Perfect divisibility and 2-divisibility’, J. Graph Theory 90(1) (2019), 54–60.Google Scholar
Gaspers, S. and Huang, S., ‘Linearly 𝜒-bounding (P 6, C 4)-free graphs’, in: Workshop on Graph-theoretic Concepts in Computer Science WG’17, Lecture Notes in Computer Science, 10520 (Springer, Cham, Switzerland, 2017), 263–274.Google Scholar
Gravier, S., Hoàng, C. T. and Maffray, F., ‘Coloring the hypergraph of maximal cliques of a graph with no long path’, Discrete Math. 272(2–3) (2003), 285–290.Google Scholar
Gyárfás, A., ‘Problems from the world surrounding perfect graphs’, Zastosowania Matematyki 19(3–4) (1987), 413–441.Google Scholar
Karthick, T. and Maffray, F., ‘Square-free graphs with no six-vertex induced path’, Preprint, 2018, arXiv:1805.05007.Google Scholar
Lovász, L., ‘Normal hypergraphs and the perfect graph conjecture’, Discrete Math. 2(3) (1973), 253–267.Google Scholar
Seinsche, D., ‘On a property of the class of n-colorable graphs’, J. Combin. Theory Ser. B 16(2) (1974), 191–193.10.1016/0095-8956(74)90063-XGoogle Scholar